
In 2011 Gov. Rick Snyder signed into law an economic incentive program known as the Michigan Business Development Program. The MBDP offers grants and other financial assistance to a small number of companies that make investments, create jobs or do some combination of both in the Great Lake State.
From March 2012 through September 2016 the program approved some 319 deals with a subsidy value exceeding $300 million, according to the authors’ count. Of that amount, $157 million had been disbursed to companies.
This study reports the results of a statistical model designed to isolate the impact that MBDP projects may have in the counties in which they are located. It relies on publicly available data from the Census Bureau and data from the state agencies that operate the MBDP. It finds the MBDP program to be ineffective: For every $500,000 disbursed through the first 10 quarters of the program — or 2.5 years — there was a corresponding cumulative loss of about 600 jobs in a county.
In 2011 Gov. Rick Snyder signed into law an economic incentive program known as the Michigan Business Development Program. It was designed to replace the Michigan Economic Growth Authority, a tax credit program created in 1995. The MBDP offers grants and other financial assistance to a small number of companies that make investments, create jobs or do some combination of both in the Great Lake State.
From March 2012 through September 2016 the program approved some 319 deals with a subsidy value exceeding $300 million, according to our count. Of that amount, $157 million had been disbursed to companies.
The program has been in existence long enough now to merit a robust examination. We built a statistical model designed to isolate the impact that MBDP projects may have in the counties in which they are located. We used publicly available quarterly workforce data from the Census Bureau and data from the state agencies that operate the MBDP. We found the MBDP program to be no more effective than the MEGA program it replaced. Specifically, we found that for every $500,000 disbursed through the first 10 quarters of the program — or 2.5 years — there was a corresponding cumulative loss of about 600 jobs in a county.
This was not a great surprise to the authors, who have conducted several economic development-related literature reviews, including a new one for this study. Many academic studies find state tax credit and subsidy programs to have little or no positive impact. Some of those studies involve programs in other states that share some characteristics with the MBDP. In addition, a close review of information available in legislative reports raises questions about the program’s performance.
One-third of MBDP deals approved during the nearly four years we studied either have been or are in some stage of default or dismissal. Not every default or dismissal was problematic, and some deals were later reconstituted. But too many of them suggests the state struggles to effectively pick winners from losers in the marketplace.
When he was first running for governor, Gov. Rick Snyder’s campaign literature stated, “Incentive programs that do not add value to economic development or aren’t worth the cost should be discontinued.” We agree, which is why our first recommendation for reform to the Michigan Legislature is to end the Michigan Business Development Program.
Here are our full recommendations:
The state of Michigan runs many programs designed to boost economic growth and development that might not otherwise occur without government intervention. These programs use targeted tax credits, tax abatements, low-interest loans or cash subsidies, among other things, for particular industries, corporations and businesses in an attempt to promote economic development.
Michigan is not alone. By one measure there are more than 1,000 economic development programs operating in the United States, most of which are at the state and local level.[1] The Kalamazoo-based W.E. Upjohn Institute for Employment Research pegged the cost of local and state business incentives in 2015 at $45 billion nationwide.[2] According to its report, the size of incentives offered by Michigan are 45 percent above the national average.[3]
There are myriad mechanisms for financing these programs, but ultimately taxpayers cover the majority of the bill. Some claim certain programs are essentially costless because jobs and the related wealth creation would not have occurred without this spending. This assertion is virtually impossible to prove and, likewise, very difficult to disprove too.
Nationwide, the modern economic “war-between-the-states” dates back to the era of the Great Depression, when Mississippi established an incentive program designed to lure northern manufacturers to invest in the state. Michigan has a long history of using public dollars to finance economic development programs too, ramping up particularly after World War II.[4]
Michigan Gov. Kim Sigler created the Department of Economic Development in 1947. Sigler argued that the state’s economy needed diversification and that this department would lead the effort. Economic diversification has been a common theme in arguments for similar programs ever since. And each subsequent governor has put his or her own stamp on Michigan’s economic development programs.[5]
More recently, Govs. John Engler and Jennifer Granholm championed new and expanded existing economic development programs and related spending. The largest of these include the Michigan Economic Growth Authority, a refundable tax credit program, the Michigan Film Incentive Program and the 21st Century Jobs Fund.
The first of these programs, MEGA, was created by Gov. Engler, expanded dramatically under Gov. Granholm and then shuttered by Gov. Rick Snyder. Gov. Granholm created the latter two initiatives, but in 2015 the film incentive program was also ended by Gov. Snyder. The 21st Century Jobs Fund spending still continues, but its form and function have changed significantly since its inception.[6]
According to the Michigan Office of the Auditor General, MEGA had offered up more than $14 billion in economic incentives during its lifetime.[7] The original MEGA law also mandated that local units of government contribute some financial or other incentive to projects MEGA funded.[8] During the first nine years of the program, those additional incentives were cumulatively worth nearly $1 billion.[9]
Gov. Rick Snyder introduced reforms to the state’s fiscal landscape in his first year as governor, 2011. Although MEGA was closed, the Snyder administration also created a new program called the Michigan Business Development Program. Designed to replace MEGA, the MBDP was similar insofar that it provided outright cash subsidies, in addition to some loans and other incentives.[*] An important difference with the MBDP compared to MEGA was that awards are not passed out through the tax code, but instead appropriated annually during normal state budget processes. This improved the transparency of this spending.[10]
The MBDP turned six years old in December 2017 and is the focus of this study. Our purpose is to evaluate the economic impact of the program in its entirety, looking at both investments the state has reported as being successful and those that have not been. In other words, this analysis weighs both the benefits and the costs of the MBDP.
This is an apt time to examine the MBDP’s structure and intent. After approving hundreds of special deals worth hundreds of millions of dollars, some economic impact from the program should be observable. We attempt to observe these impacts with this analysis.
[*] Technically, MEGA was a tax credit program, but it allowed for refundable tax credits which ultimately provided cash subsidies to companies. “Public Act 250 of 2011” (State of Michigan, Dec. 13, 2011), 2, https://perma.cc
The original law establishing the Michigan Business Development Program — which has already been amended — contains key mandates authorizing the state to “provide grants, loans, and other economic assistance to qualified businesses” that create jobs or make certain investments in the state.[11] The MBDP is run by the Michigan Strategic Fund and the Michigan Economic Development Corporation.
The MSF was created by Gov. James Blanchard and is the entity to which state appropriations are made to fund many economic development programs, including those administered by the MEDC. It has its own board and — according to the MEDC — is now directly responsible for the majority of the state’s economic development programs.[12]
The MSF is responsible for approving the grants, loans and other economic assistance provided through the MBDP. The MBDP law mandates a number of key items, which include but are not limited to, giving assistance to businesses that are or will be located in the state of Michigan, publishing a process for applying and being approved for state subsidies and disclosing this activity. Any company approved for such favors must sign an agreement detailing what is expected of it in order to receive help from the state. Each agreement compels an audit of certain information by the state to ensure that detailed stipulations are met. No recipient may collect in excess of $10 million for a particular project.[13]
In addition, the state mandates some type of contribution — “staff, financial or economic commitment” — from the local unit of government with jurisdiction over the location where the project will occur.[*] The receiving entity must also show a need for state assistance and agree that it is willing to provide “data described in the written agreement necessary for the fund to report.”[14]
There are also transparency requirements for the Michigan Strategic Fund overseeing the program. Officials must post online information about each agreement, including the name and location of each business in the program.[15]
In addition, the MSF must report to the Legislature annually on the activities of the MBDP. The annual report must include the amount a business will invest as part of its agreement with the state, the number of new jobs committed and the number created to date, the amount awarded and disbursed to each company to date and the total number of new agreements per year. It must also indicate if the project is for a new business or an expansion and whether the business is relocating from another state.[†]
Lastly, and of particular note, the state mandates that “an evaluation of the aggregate return on investment that this state realizes on the actual qualified new jobs and actual qualified investment made by qualified businesses.”[16] This entry was worth quoting in its entirety. The state uses a software model to forecast the return on investment associated with the MBDP subsidies and other incentives.[17]
[*] MCL § 125.2088r(3)(a). As just one example, the MBDP deal for Spiech Farms includes a contribution of “staff time” from Southwest Michigan First, a local economic development agency, in support of an expansion project in Paw Paw, Mich. The state offered the company a $220,000 subsidy through the MBDP. “Project Summary: Spiech Farms” (Michigan Economic Development Corporation, 2016), https://perma.cc
[†] MCL § 125.2009. The original law mandated that reports to the Legislature also include the education backgrounds of people hired by the businesses as part of those respective deals and whether or not they moved from out of state. This is no longer the case. Also, MSF’s reporting requirements are now consolidated in one statute and the MBDP statute no longer contains its own separate reporting requirement. “Public Act 250 of 2011” (State of Michigan, Dec. 13, 2011), https://perma.cc
By our count, there have been 319 deals approved between March 2012 and Sept. 29, 2016, valued at more than $300 million. Only $157 million of that total has actually been disbursed through Sept. 29, 2016.[18]
The largest, single deal involved a $10 million loan to M1 Rail in Wayne County; the smallest, just a $100,000 subsidy to both Avon Protection Systems, Inc. in Wexford County and Neogen Corporation in Ingham County.[19]
The average deal was worth more than $950,000; the median, $500,000.
Although 43 Michigan counties are home to at least one MBDP approved project through September 2016, 55 percent of all deals occurred in just four counties: Oakland, Wayne, Kent and Washtenaw. The vast majority of these were subsidies in the form of grants.
Graphic 1: MBDP Deals by County, 2012-2016
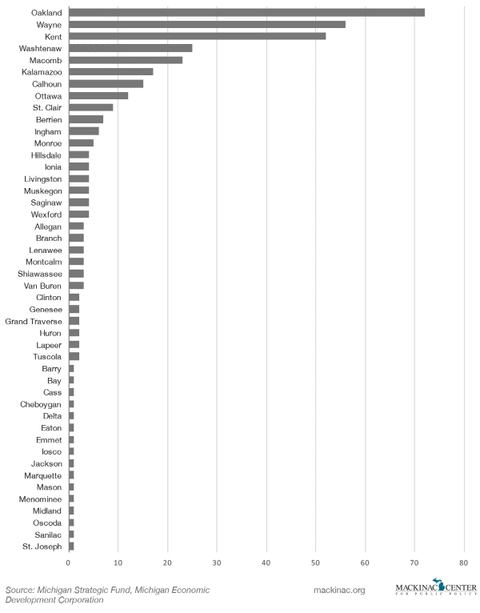
The fiscal year 2016 MSF-MEDC annual report to the Legislature indicates that only four deals were identified as “loans.”[*] Two of these loans went to companies that also received outright grants. Another 11 deals were labeled “other” (one of which included a grant) but the legislative report doesn’t offer details on exactly what “other” type of financial assistance means.[20] One can discover those details in different state documents, however. As one example, Cosworth, LLC was offered a loan at 1 percent interest that may also be forgivable depending on how many new jobs it creates in excess of 50 by a certain date.[21]
The value of incentives approved for all deals through the MBDP in the fiscal 2016 report totals $277.6 million. These totals include most deals struck in previous years, but revoked deals are removed from tallies listed in the annual legislative reports. Of the 274 MBDP projects identified in the 2016 report with executed agreements, 81 percent involved an expansion of an existing company and location as opposed to creation of a new facility or relocation of production from elsewhere, such as from another state.
Of all approved MBDP projects tallied by us between March 2012 and September 2016, more than 33 percent are in or have been in some stage of default or have been dismissed and terminated.[†] It appears from the annual reports that “default” means that the companies have failed to meet some type of agreed upon stipulation or milestone. It is not unreasonable to assume that the number of revoked deals would be much higher if administrators were not quick to accommodate some failure by the company to live up to the original the terms of an agreement.[‡]
As evidence, the 2016 MSF-MEDC report indicates that the state offered 38 amendments for MBDP agreements in that fiscal year. Of those 38, 28 appear to explicitly lower some previously agreed upon performance threshold or milestone. For instance, the entry for SL American Corporation says, “extended minimum [qualified new jobs] date from [Jan. 1, 2016, to Sept. 30, 2016] and extended remaining milestone due dates.”[22]
In other words, the MSF mandates a certain level of performance in its agreement with companies but then later lowers the bar. To the MSF’s credit, in many cases they also reduced the size of the grant offered to the companies that benefited from amended agreements.
Two deals in the fiscal 2016 report contain a mixture of lowered and raised thresholds, extending the time a company had to create qualified new jobs, in one example, but also raising the number of new jobs that the company agreed to create. Another seven we can only categorize as an “amendment” due to the vague nature of the language in the annual report. For instance, the Shepherd Caster Corporation had its “local support requirement” amended, but the MSF-MEDC annual report does not detail the change.[§]
The 33 percent rate at which MBDP companies might be in default or dismissed from the program outright might actually be higher for another reason. Our totals include MBDP deals through September 2016 only, but deals struck by the state with companies typically give some length of time — such as six months or a full calendar year — to reach some type of milestone, such as new job creation. In other words, the most recent MBDP companies in our totals have not yet had a chance to fail and be officially reported as such.
An MEDC spokeswoman last October informed one author, LaFaive, that at least eight more companies have had their incentive approvals revoked and which will be announced in the 2017 fiscal year report to the Legislature and released in 2018.[23]
All of these items are important considerations for assessing the effectiveness of the MBDP.
[*] The reader should note that the annual report produced by the Michigan Strategic Fund and Michigan Economic Development Corporation for the Legislature only covers MBDP data from inception through September of 2016 in its master spreadsheet of deals. Other documents published by the agencies allow us to measure the value of MBDP offers further out. “MSF/MEDC Annual Report to the Legislature, FY 2016” (Michigan Economic Development Corporation, March 15, 2017), https://perma.cc
[†] We choose to truncate our totals to fiscal 2016 for this narrative for two reasons. First, doing so provides us with more consistent data from the agencies themselves as to the status of their program. Second, our own statistical analysis employs public data from the federal government that is only available through calendar-year 2016.
[‡] Our count of approved projects differs slightly from the fiscal 2016 report to the Legislature because we still include those projects that have been revoked. The MSF-MEDC fiscal report removes these deals from its master spreadsheet. Four annual reports (fiscal 2013 through fiscal 2016) suggest a total of 40 approved projects were revoked and often for nonperformance. The fiscal 2016 report lists nine revocations and seven say the “company was unable to meet milestone requirements.” There is one exception. We omit Covisint, LLC, from our count of dismissed deals. We learned late in the production of this study that the deal was approved, but then later “mutually terminated.” Emily Guerrant, senior vice president of marketing and communications, Michigan Economic Development Corporation, email corresponce with Michael D. LaFaive, senior director of fiscal policy, Mackinac Center for Public Policy, Jan. 30, 2018.
[§] “MSF/MEDC Annual Report to the Legislature, FY 2016” (Michigan Economic Development Corporation, March 15, 2017), 13, https://perma.cc
The MEDC routinely publishes press releases that announce the number of jobs that will allegedly be created as a result of subsidies offered by the MBDP. For example, on May 23, 2012, the MEDC announced in a press release that four MBDP deals had been approved by the MSF and claimed the companies — Center Manufacturing, Huntington Foam, LLC, MedDirect, Inc. and Muskegon Castings Corp. — would create a total of 465 jobs and as much as $15.7 million in new investments. The headline reads: “Four Michigan Businesses Receive State Support to Expand, Add Jobs.”[24]
The MSF-MEDC 2016 annual report to the Legislature says that $156.7 million in grants and loans and “other economic assistance” were disbursed to MBDP companies. Because of these subsidies the annual report credits the MBDP with 17,913 “actual new jobs created” throughout the life of the program.[25]
Reporting this data is required by law and includes an analysis using a software model called REMI that attempts to measure the dynamic effect that such investments and new employment will create going forward.[*] For example, in the 2016 annual report, the introduction of the MBDP states:
The aggregated projected return on investment to the state of Michigan for the projects approved for FY 2016 is 10.0. This means that for every $1 invested, there is a projected return of $10.00. The formula is based on the anticipated amount of overall cash flow to the state through new personal income generated by the projects.”[26]
In other words, the state is claiming that for every dollar it offers up to these companies, its coffers receive $10 in return.[27] The short methodology described in the annual report indicates that it uses “projected personal income generated through direct jobs created by the companies, indirect jobs as a result of the projects and projected capital investments.”[†]
One significant issue about the forecasts is that each deal’s impact is calculated in such a way where it would be all but impossible to show a negative return on investment. This is so because the REMI estimates are made with the presumption that the expected job creation will become a reality and that no jobs would be created and no investment would be made without the subsidy.
For example, Adient US, LLC’s REMI input assumption worksheet presumes a certain level of job creation (115) at a certain pay scale with fringe benefits. But we have repeatedly pointed out, program administrators’ cannot prove that these jobs and larger investment would not have been created anyway, without taxpayer subsidies.[28]
It is worth noting here that the MSF-MEDC aggregate projected return on investment is calculated simply by adding up the total ROI projected on each deal and dividing by the number of deals made during the period.[29] This is important for placing annual state projections of the MBDP’s alleged success in its annual reports in perspective.
In sum, the state is basically inputting optimistic project results into the REMI model. The result is an optimistic output for each deal. These results are then summed up and averaged for the year-end report to the Legislature.
There are other reasons to consider suspect claims of job creation made by the state through the MBDP. These are listed and explained below.
1. Neither the MSF nor the MEDC can prove that the company was not going to locate or expand in Michigan without their incentives.
This is a paramount presumption to any claims of success made by the state. It is naïve to assume that every company would not have located to or expanded in Michigan and created jobs if it were not for the MBDP. Yet in the agencies press releases and job and investment accounting for its annual report to the Legislature this seems to be the presumption.
In a brief explanation of the program online, the MEDC writes that the subsidies and loans are for “highly competitive projects in Michigan.”[30] Program administrators seem to suggest that they can ferret out the most competitive and best of these and then subsidize them to the advantage of Michigan’s economy. There are reasons to doubt such a viewpoint.
In early 2017 the Kalamazoo-based W.E. Upjohn Institute for Employment Research published a multistate economic development incentive database and related analysis.[31] The database contains information from 1990 to 2015 and includes incentives such as property tax abatements and different types of tax credits (jobs, investment and research and development) as well as some job training programs.
The author of the analysis, Timothy Bartik, wrote in a summary that, of all the incentives in their database, it appears that only about 6 percent were effective at actually changing the behaviour of firms. In other words, 94 percent of expansions would likely have happened anyway without the state dangling targeted incentives in front of companies.[32] Bartik writes:
Incentive differences do not appear to have large effects on state economic growth by industry. The database suggests incentive effects toward the low end of prior estimates: the average incentive package, 1.4 percent of value added, might tip the location decision of 6 percent of incented businesses — the other 94 percent of the time, the state would have experienced similar growth without the incentive.[‡]
If that same rate of successfully incentivized companies applied to the MBDP than $147.6 million of the $157 million expended in corporate subsidies through fiscal 2016 was essentially wasted. Even then, the value of winning expansions and new jobs from the 6 percent of deals may still not be a net plus from the state when you consider the opportunity cost of doing so. Opportunity cost is the value of the next best alternative use of the money the state spent providing these incentives.
In addition to modeling each MBDP deal, the state should use the REMI model to demonstrate some type of counterfactual. For instance, how many jobs would be created if the state dedicated $300 million to personal or corporate income tax cuts, infrastructure investments or some other basket of public goods purchased at taxpayer expense? A well-designed counterfactual scenario or two may place the alleged ROI of the MBDP in a different perspective.
2. The REMI model’s output is at best only as good as its input.
Because the state makes projected estimates of the ROI for individual deals and the overall program, any deal that fails outright, or is even modified after a forecast is made, would have changed what the MSF-MEDC could have reported to the Legislature.
For example, if Adient was projected to create 115 jobs at a particular wage rate, but instead only created 70, or didn’t create any at all, the tally of projected ROI would change but not necessarily be reflected in the annual report to the Legislature.
It is unlikely all of the dismissals and amendments would have come at such a time as to be worked into the proper year for which the state’s annual projected ROI estimates were made. Given these facts it is probable, even highly likely, that the program’s ROI as estimated by state is overstated and perhaps by a wide margin. Also, legislative reports to date make no mention of modifications to REMI input based on amendments or revocations.
According to the state’s last three annual reports, 34 MBDP projects were revoked through September 2016.[§] Moreover, many program deals were modified in such a way as to reduce the grant size, job creation targets or other mandates. Reduced investments and hires would reduce the purported projected values of these deals.
3. REMI forecasts for similar programs in the past proved to significantly inflate the ROI of those programs’ spending.
Even when used responsibly and with good input data, the REMI forecasts will not necessarily produce forecasts that are accurate. The MEDC has repeatedly claimed success for programs that proved to be nothing of the sort and did so on the basis of REMI analyses. Consider some examples.
The state of Michigan paid consultants for years from the University of Michigan to use REMI to measure the effectiveness of the Michigan Economic Growth Authority program.[33] This program approved deals from 1995 to 2011 and these published REMI analyses showed positive impacts, frequently large ones.
Each MEGA deal typically came with an “Economic Effects” memo that pointed to the number of jobs and wealth that would allegedly be created as a direct result of the refundable tax credit deal struck by the state and some company. Yet the program and its job creation prowess turned out to be a failure by several measures.
There have since been five rigorous studies of the now-defunct MEGA program done by independent scholars. Four of them suggest the program had a zero to negative impact. One, published in Economic Development Quarterly academic journal, showed a range of possible outcomes and was largely positive. It was performed by running simulations using the REMI model.
Two of the studies were published by the Mackinac Center for Public Policy in 2005 and 2009. The first was titled “MEGA: A Retrospective Assessment” and the second “Michigan Economic Development Corporation: A Review and Analysis.”[34] The third was published in 2010 by the Anderson Economic Group of Lansing and titled “Effectiveness of Michigan’s Key Business Tax Incentives.”[35]
The fourth study was published in The American Review of Public Administration journal in 2013 by Michigan State University scholar Laura Reese and was titled “If All You Have is a Hammer: Finding Economic Development Policies that Matter.”[36]
The fifth — and only study with a positive showing for the MEGA program — was performed by the W.E. Upjohn Institute out of Kalamazoo and published in 2014. This study, titled “Simulating the Effects of the Tax Credit Program of the Michigan Economic Growth Authority on Job Creation and Fiscal Benefits,” found the program “appears to have had large effects on job creation relative to its net fiscal costs.”[37]
Why might the individual projected and aggregate sum of the MEGA projects not square remotely with that of academic and most other scholars? The simplest explanation is that REMI forecasts are just that: forecasts. They rely on economic assumptions that not only could be wrong, but also rely on underlying economic conditions that may start changing the moment a REMI user finishes an estimate.
[*] MCL § 125.2009(5)(e). The REMI software is a popular program with governments and their consultant contractors. It has been used to forecast the purported successes of the closed Michigan Economic Growth Authority and Michigan film incentive programs.
[†] The software program, REMI, was also used for reports predating fiscal 2016 and the agency’s reported projected ROI’s for every dollar spent of $10.35 (2015); $8.72 (2014) and $7.60 (2013).
[‡] It is worth noting here that the Bartik summary, cited above, also argues that higher benefits to incentives than he cites may be achieved by incenting high-technology or high-wage industries. He also writes that “incentives are more effective if they are more up front.” This is a characteristic of the MBDP, as the subsidies can be earned in relatively short order. Timothy J. Bartik, “Better Incentives Data Can Inform Both Research and Policy” (W.E. Upjohn Institute for Employment Research, April 2017), 2, https://perma.cc
[§] The total may actually be 33 as the MSF-MEDC fiscal 2014 and 2015 reports both show “Cataphora, Inc.,” as having been revoked. “MSF/MEDC Annual Report to the Legislature, FY 2016” (Michigan Economic Development Corporation, March 15, 2017), 15, https://perma.cc
The proliferation of economic development programs run by state and local government has allowed academics of every stripe and locale ample opportunity to study the respective impacts of such programs. There is rarely unanimity about any broad topic under study in academe. On the subject of economic development, however, it seems fairly clear from research by scholars across the country that results from such programs on balance are not positive.
This review describes a cross section of the research literature in both a broad and narrow sense. It is not meant to be the last word on the state of academic literature. It is to provide the reader with a perspective on past and current efforts to quantify economic development programs broadly and over time, including those with characteristics relevant to the Michigan Business Development Program.
For a wider take on incentive-related literature, the authors recommend reading the literature reviews and technical appendices of three previous Mackinac Center for Public Policy studies. These include, “MEGA: A Retrospective Assessment” (2005); “The Michigan Economic Development Corporation: A Review and Analysis” (2009); and “An Analysis of State Funded Tourism Promotion” (2016), as well as the two studies referenced in footnotes below.[*]
It is customary in academic papers to review the literature that has proceeded some new scholarship. In some instances scholars dedicate an entire paper to reviewing the existing literature on a topic and categorize and sum its findings for other researchers. These are commonly called a “meta-review.”
One of the broadest and most cited economic development meta-reviews was published by Peter Fisher and Alan Peters in 2004. According to Google Scholar it has been cited in 301 other works.
The paper, titled “The Failure of Economic Development Incentives,” was a review of published analyses of state and local economic development programs. Its authors hoped to answer three major questions:
1. Do business incentives actually cause states or localities to grow more rapidly than they would have otherwise? 2. If so, is the growth targeted so as to provide net gains to poorer communities or poorer people, or is it merely a zero-sum game? 3. How costly to government is the provision of these incentives compared to alternative policies?[38]
Their conclusion is that despite the massive costs associated with running state and local economic development programs there is little evidence to suggest job and wealth creation for anyone, let alone the poor or for the governments running these programs. From their conclusion:
On the three major questions ... traditional economic development incentives do not fare well. It is possible that incentives do induce significant new growth, that the beneficiaries of that growth are mainly those who have greatest difficulty in the labor market, and that both states and local governments benefit fiscally from that growth. But after decades of policy experimentation and literally hundreds of scholarly studies, none of these claims is clearly substantiated. Indeed, as we have argued in this article, there is a good chance that all of these claims are false.[39]
Since this was published in 2004 there have been many additional economic development studies published in peer-reviewed journals across the country. The conclusions are mixed — as is often the case with academic studies — but it seems that, overall, they still lean toward skepticism that such programs are effective.
A 2017 project by the W.E. Upjohn Institute for Employment Research — mentioned above — involved creation of a new publicly accessible and transparent database of economic development incentives. This database, which contains information from 1990 to 2015 covers 45 industries from 33 states, and will help researchers better measure the impact of incentives across states and types of incentives.[40] It finds that “[i]ncentives do not have a large correlation with a state’s current or past unemployment or income levels, or with future economic growth.”[41] These findings are qualified in that the research “does not include many other control variables, which might alter results.”[42]
In a forthcoming paper titled, “Do Business Subsidies Lead to Increased Economic Activity? Evidence from Arkansas’s Quick Action Closing Fund,” authors Jacob Bundrick and Thomas Snyder examine cash “deal-closing funds” and their use to spur economic development in Arkansas. The authors report finding scant evidence for programmatic success. Consider the key findings from the conclusion of their working paper:
Our within-county models estimate the four-year cumulative effect of [Quick Action Closing Fund] subsidies. These models offer no evidence to suggest that providing QACF subsidies to businesses within a given county provides the county with any significant cumulative private employment and establishment benefits. Furthermore, the models fail to offer evidence of a significant cumulative employment spillover effect related to the QACF subsidies provided to businesses in a county’s bordering counties. However, we do find evidence of a statistically significant, but economically small, negative cumulative establishment spillover effect related to the QACF subsidies provided to businesses in a given county’s bordering counties. Accounting for the fiscal costs of the program, though, yields no significant relationship between the QACF and county-level private employment and establishments. Finally, our cross-county estimations find little evidence to suggest that the QACF, on average, explains differences in private employment and private establishments at the county level.[43]
This research has implications for our study of the MBDP. Arkansas’s QACF program shares characteristics of the MBDP. First, it is a cash subsidy program. Second, the QACF is designed for use in “highly competitive situations.” The MBDP likewise is described by the MEDC as “economic assistance for highly competitive projects” and “preference may be given to businesses in need of additional assistance for deal closing and second stage company gap financing.”[44] Lastly, the authors attempt to measure relationships between the subsidy program and county employment, and we do likewise.
Another 2017 paper looked at economic development incentives offered through programs run out of Virginia and Maryland between 2006 and 2012.[45] To analyze the impact of each, the author created a group of firms that would serve as a control on his estimates. That is, he would attempt to measure the performance of incentivized firms against a like control group of firms that had not received fiscal favors.
The Virginia program — Commonwealth Opportunity Fund — is a deal-closing fund such as the QACF in Arkansas. Like the MBDP this program too hands out grants and loans and oversees recipient performance. They can also cancel deals and demand a “clawback.” Clawback provisions allow units of government to demand the return of subsidies for failure to meet requirements of an agreement. The MBDP has cancelled deals and demanded that its subsidies be returned too, though to varying degrees.
The Maryland program studied in this paper provides a mix of different incentives that qualify as economic development. Nathan Jensen, the author of the paper, just focused in on those incentives associated with job creation and investment efforts for business, much like the MBDP.
Jensen writes that his “findings cast considerable doubt on the effectiveness of these programs in generating new employment in the short run.”[46] The incentives “have no discernable impact on job creation, which is consistent with previous studies.”[47] He also found excluding firms that had been subject to a clawback provision — presumably for poor performance or “non-compliance” — does not improve the net performance of the programs studied.
Neighboring Pennsylvania runs a “Redevelopment Assistance Capital Program” that hands out cash grants to businesses that move to or expand in the Keystone State. Since 1986 the program has approved $5 billion in grants for 2,200 projects, according to the Mercatus Center, a think tank housed at George Mason University.[48]
The Mercatus study looks at the impact of grants from 2010 — the largest approved expenditure in the program’s history at more than $1 billion.[49] More than $600 million of that was paid out and the author found “a small, positive effect on county employment growth from 2010-2013.” The author adds, however, “this result should be interpreted with caution since it does not represent net jobs created across the state.”[50]
A 2014 National Tax Journal article tackled the question of whether or not increasing the availability of nontax incentives such as “cash and near-cash grants, low-interest financing, free land and buildings, etc.” meant more jobs.[51] The author examined the question using a dataset that ran from 1970 to 2002 and attempted to measure employment growth and level in U.S. counties. She concluded:
[I]ncreasing the availability of non-tax incentives negatively affects medium-term rural employment. There appears to be no effect otherwise, although it is possible that there may be small short-term benefits to urban county employment levels. The finding of negative or no effect calls into question the generally accepted practitioner view that providing more economic development incentives to attract capital will result in more jobs.[52]
[*] A classic work in the incentive literature is a 2001 paper by Terry F. Buss and published in Economic Development Quarterly. Terry Buss, “The Effect of State Tax Incentives on Economic Growth and Firm Location Decisions: A Review of the Literature,” Economic Development Quarterly 15, no. 1 (2001): 90–105. For a highly readable summation of literature surrounding the political economy of targeted incentives, see Christopher J. Coyne and Lotta Moberg, “The Political Economy of State-Provided Targeted Benefits,” Review of Austrian Economics 28 (June 1, 2014): 337–356, https://perma.cc
To best measure the economic impact of the Michigan Business Development Program we have constructed what is known as a “spatial panel vector auto regression,” or PVAR, model. A full description of the technical aspects of this model and related output can be found in “Appendix A: Modeling the MBDP’s Economic Impacts.”
The model is constructed using data from the U.S. Census Bureau’s Quarterly Workforce Indicators from 2012 through 2016 and from data found in reports published by the MSF and MEDC. The QFI data capture the start of the MBDP as marked by its first approved deals and include the latest available quarterly data from the Census Bureau at the time of this writing. We use data from MSF and MEDC reports that span the life of the program, from these agencies’ MBDP “projects lists” and each MSF/MEDC annual report to the Legislature through Sept. 29, 2016. These documents were occasionally supplemented by information provided by an MEDC spokesperson.
We are particularly interested in the county employment effects of the MBDP program since its potential to create new jobs is how the program is marketed and defended. Our examination of county-level employment is useful because most MBDP awards are specific to one county, where new investments and job creation allegedly occurs.[*] Indeed, MEDC press releases, related news coverage and official state reports all seem to emphasize this angle of the program’s economic development results.
Evaluating the effect of incentives is a challenge. For instance, the timing of state investments and related subsidy payments influence the process of measuring their impacts, and these payments are paid out on an individual basis to each firm receiving state support. The unique geographic factors experienced by each firm further complicates the procedure.
Another concern is the possibility that firms seeking these incentives are not entirely random — that there’s something unique about them as a group. Perhaps, for instance, firms selected for subsidies are more likely to choose certain places to locate or expand their business than would otherwise be the norm. If these choices deviate from what should be expected without the influence of the MBDP, this risks biasing the estimated impact. Additionally, there may be something intrinsic to particular counties that make them more or less likely to contain firms that receive incentives. This, broadly speaking, is known as endogeneity bias, and it is a challenge for assessing incentive programs of all kinds.
To address this issue, we use a very flexible econometric model that allows the impact to materialize at different speeds. We favor this model since it allows us to test endogeneity, the technical problem arising from reverse causation, which may occur when incentives are provided to firms that choose their location on a nonrandom basis. We include a “spatial,” or geographic, component for most estimates because labor markets cross county borders.
The advantage of our approach — as opposed to the program administrators’ REMI-based model — is that we employ historical information about what has occurred. The state’s REMI forecasts rely on assuming information about both the future performance of the company receiving subsidies and the underlying economic conditions impacting the firm. In other words, our model relies on data based on observed reality, whereas the state relies on data based ultimately on predictions about the future.
[*] It is possible that some firms receiving MBDP support are credited for creating jobs outside the county in which their MBDP project is located. Further, some firms (by our count there are only eight) get support for projects located in more than one county. Some companies were allowed to count jobs created “statewide.” The impact of the potential employment growth from these types of projects may not be captured in our model if the new jobs were created in counties that did not host any other MBDP projects. We do not expect that these situations would significantly impact our findings.
The MSF-MEDC reports that the MBDP program disbursed $156.7 million and helped create 17,913 jobs. That works out to a cost of about $8,747 per job. The findings of our model, however, produce no statistically reliable positive impact of MBDP incentives on employment.
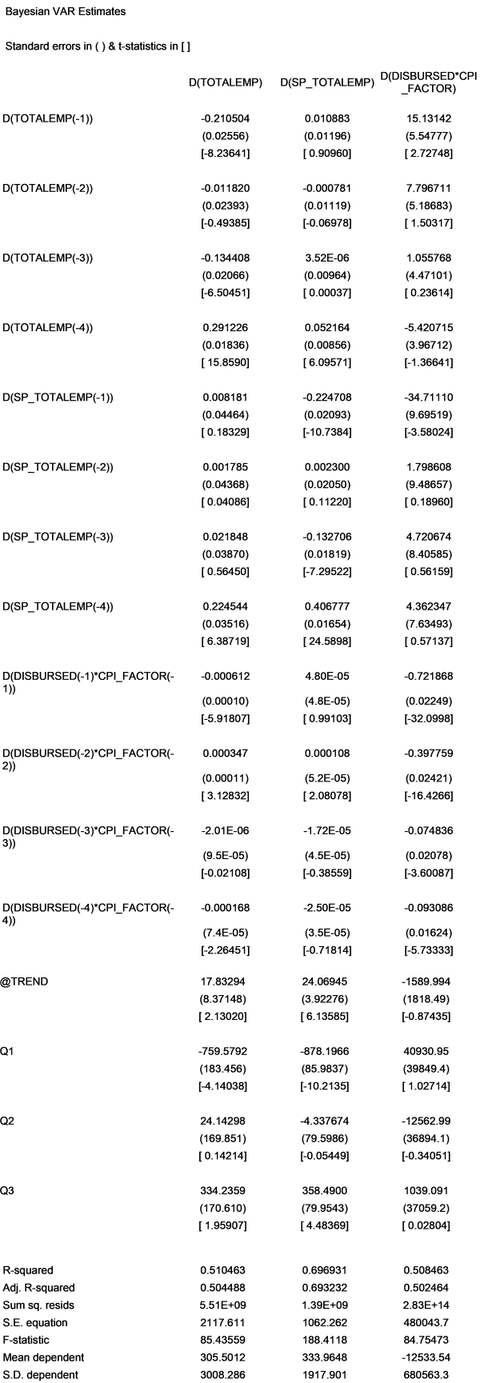
Our first estimation involved the cumulative employment effects over time in counties with MBDP projects. We find a slightly negative impact, showing a loss of about 600 jobs per $500,000 of MBDP incentives. This is the cumulative result after 10 quarters, or two-and-a-half years, of the program’s operation. Even using a slightly different version of the PVAR model, the results are similar, finding effects that were not statistically significant different from zero. (See the technical appendix for more information.)
Measuring the total employment impacts of the MBDP by county was the focus of this statistical model, but we also dove deeper given the makeup of MBDP projects. Most MBDP dollars are allocated to manufacturing firms. We looked again at the data just zeroing in on the impact the program might have on the manufacturing sector and we found a similar outcome: The cumulative impact on total employment in manufacturing over 10 quarters due to MBDP incentives produced no statistically significant or economically meaningful impact based on our models.
In sum, the results of our model show that the impact of MBDP projects on total employment in a county was negative: For every $500,000 worth of disbursed incentives, counties lost about 600 jobs. The results based just on manufacturing firms produced a better result statistically, but it wasn’t a net positive. The clearest interpretation of this work is that our model found no statistically meaningful impact on manufacturing jobs from MBDP incentives.
It may seem counterintuitive that giving select companies $500,000 actually leads to a reduction in total jobs in a county. But there are plausible explanations for this reality. One could be that firms receiving MBDP grants are crowding out other projects in a county that would have had a larger positive economic impact. Another possibility is that other incentives provided by local economic development agencies — which are required to participate in MBDP projects — are producing these negative externalities. These local incentives may have the effect of driving up tax rates on firms not receiving MBDP grants and producing a net loss in jobs for the county.
These are speculations — we were not able to measure or test the crowding out effect or the potential negative effect local economic development initiatives may create. But what our models suggest is that doling out MBDP grants to firms is not having a positive impact on jobs in a county. Unobserved effects must be crowding out or nullifying the impact of MBDP grants. These results should encourage policymakers to reassess the value of this program.
The MSF-MEDC reports that the MBDP program disbursed $156.7 million and helped create 17,913 jobs. That works out to a cost of about $8,747 per job. The findings of our model, however, produce no statistically reliable positive impact of MBDP incentives on employment.
Our first estimation involved the cumulative employment effects over time in counties with MBDP projects. We find a slightly negative impact, showing a loss of about 600 jobs per $500,000 of MBDP incentives. This is the cumulative result after 10 quarters, or two-and-a-half years, of the program’s operation. Even using a slightly different version of the PVAR model, the results are similar, finding effects that were not statistically significant different from zero. (See the technical appendix for more information.)
Measuring the total employment impacts of the MBDP by county was the focus of this statistical model, but we also dove deeper given the makeup of MBDP projects. Most MBDP dollars are allocated to manufacturing firms. We looked again at the data just zeroing in on the impact the program might have on the manufacturing sector and we found a similar outcome: The cumulative impact on total employment in manufacturing over 10 quarters due to MBDP incentives produced no statistically significant or economically meaningful impact based on our models.
In sum, the results of our model show that the impact of MBDP projects on total employment in a county was negative: For every $500,000 worth of disbursed incentives, counties lost about 600 jobs. The results based just on manufacturing firms produced a better result statistically, but it wasn’t a net positive. The clearest interpretation of this work is that our model found no statistically meaningful impact on manufacturing jobs from MBDP incentives.
It may seem counterintuitive that giving select companies $500,000 actually leads to a reduction in total jobs in a county. But there are plausible explanations for this reality. One could be that firms receiving MBDP grants are crowding out other projects in a county that would have had a larger positive economic impact. Another possibility is that other incentives provided by local economic development agencies — which are required to participate in MBDP projects — are producing these negative externalities. These local incentives may have the effect of driving up tax rates on firms not receiving MBDP grants and producing a net loss in jobs for the county.
These are speculations — we were not able to measure or test the crowding out effect or the potential negative effect local economic development initiatives may create. But what our models suggest is that doling out MBDP grants to firms is not having a positive impact on jobs in a county. Unobserved effects must be crowding out or nullifying the impact of MBDP grants. These results should encourage policymakers to reassess the value of this program.
This program was designed to replace a previous, larger refundable tax credit program that cost the state billions without producing much in the way of net new jobs. After six years in operation, the first measures of the Michigan Business Development Program’s effectiveness are in. It would appear that this program is not achieving its intended goals. A majority of the subsidies are likely handed out to companies that would have expanded in or moved to Michigan anyway, and these projects are potentially crowding out better investments. Despite claims to the contrary, the MBDP does not create net new jobs for Michigan citizens.
Eliminating this program would be precisely what Gov. Rick Snyder proposed to do with failed state economic development programs when he was running for his first term as governor. His campaign literature, “Rick for Michigan: Reform The Michigan Economic Development Corporation,” reads: “Incentive programs that do not add value to economic development or aren’t worth the cost should be discontinued.”[53] We agree and the MBDP appears to fit that description.
2. Prohibit amendments to relax milestones.The state offers up subsidies to companies that agree to meet certain job creation and other milestones by certain dates and then repeatedly relaxes those standards. They should not. At question here is the state’s ability to allegedly pick winners from losers in the marketplace. The ability to relax agreed upon standards of performance artificially raises the “success” profile of state officials and their purported ability to invest public dollars in just the right private businesses.
3. Cease unqualified claims of high returns on investment.In each year’s annual report the state makes claims of projected success that strain credulity. The fiscal 2016 report claimed a $10 return for every $1 invested by the program. Yet we know that projections — using the REMI model — are based on presumptions of success that often do not pan out the way the state presumes it will. The Mackinac Center for Public Policy’s analysis, which uses historical as opposed to projected data, suggests the program does not create net new jobs.
4. Mandate a counterfactual analysis.For the sake of perspective, mandate that the MSF and MEDC use the REMI model to analyze alternative uses of the MBDP subsidies. What if, instead of giving companies $50 million a year, the funds were instead used to buy some other basket of public goods, complete an infrastructure project or cut personal income taxes? Using the model thus would put claims of large scale job creation from MBDP projects in greater perspective.
5. Improve the transparency of the program.The MSF obfuscates its poor choice of investments by expunging dismissed companies from its master count of deals in each year’s annual report to the Legislature. It should not. Companies that have been dismissed — or have ever been in default, for any reason — should be explicitly maintained in each year’s report. Reporting requirements make no mention of the process for expunging projects and removing them is inimical to the purpose of reporting. These reports are supposed to provide the clearest picture of program performance, not just a vehicle to cite purported success stories. Including data each year on every failed deal, both present and past, will provide a quick reference and perspective to lawmakers on the ability of state development officials to actually pick winners from losers in the
[*] “Rick for Michigan: Reform the Michigan Economic Development Corporation” (Rick Snyder for Michigan Committee), https://perma.cc
The Michigan Business Development Program, like its predecessor program, the Michigan Economic Growth Authority, is ineffective at creating jobs. We find that there is actually a negative jobs impact resulting from the MBDP.
It is best to dismantle this program now, lest it continue to waste public dollars. The state would have likely been in a better position fiscally had it eliminated the ineffective Michigan Economic Growth Authority or film subsidy programs when analyses of them showed them having no positive impact on the state’s economy. It is particularly important given the birth of two new subsidy programs adopted by lawmakers in 2017 and known as “MI-Thrive” and “Good Jobs for Michigan.” These programs are designed to benefit large corporations and developers but suffer from the same shortcomings as other failed state economic development programs in and outside of the Great Lake State.
The $300 million-plus approved for distribution to select businesses through September 2016 would be better spent elsewhere. About 33 percent of the deals approved by the MSF between March of 2012 and through Sept. 29, 2016, have been or are in some stage of default or dismissal. The statistical approach developed for this study suggests that the program’s performance is even worse. Policymakers should reconsider it entirely.
The Michigan Business Development Program targets employment impacts, thus evaluating the effect MDBP credits on total and sectorial employment offers potential for understanding better the employment dynamics related to the incentive. To perform this analysis we will model impacts on a short time period of quarterly data from 2012-Q1 through 2016-Q4. The data are drawn from MSF-MEDC reports on individual firms and the Quarterly Workforce Indicators on employment and employment by sector.[1]
We use a spatial panel vector autoregression, or PVAR, to test the relationship between MBDP grants and county-level employment. To evaluate the dynamic relationship between this economic development incentive and employment we compute and report the impulse-response function.
The use of a PVAR is appropriate when assuming an unknown level of endogeneity between the variables, and thus employs a series of lagged variables to compute the effects. We do however assume an ordinal nature of endogeneity, thus the order of estimation proceeds with the incentive, then employment and finally spatial employment. This ordering of the variables is a Bayesian approach (see Caldara and Kamps, 2008; Lof and Malinen, 2013).
A few econometric considerations are appropriate in constructing the details of a spatial PVAR. First the variables of interest are nonstationary.[2] This necessitates the use of first differenced variables, which reduce some to the potential structural relationship between variables. However, since we are evaluating the impact of the incentive on employment this is not cause for worry and we discuss a departure from the Bayesian approach in the results section.
This time period was one of economic recovery from the Great Recession of 2007-2009, so growth in manufacturing employment should be expected. That necessitates the use of an exogenous trend, and the quarterly frequency of the data argues for seasonal dummies, which we employ in Q1-Q3. The lag structure was chosen through the minimization of the Akaike Information Criterion and selected at eight quarters from the announcement date.
The construction of the spatial lag was done using the first order contiguity matrix, W, so that for each county i, the population weighted average of these variables are calculated for contiguous counties. Economic applications of this appear in Hicks and Wilburn (2001) and Hicks and LaFaive (2011).
Thus, the spatial panel vector autoregression takes the form:
Ζi,t = a + δΖi,t-n + βγt + ei,t (1)
where:
Ζi,t is the first differenced values of the endogenous variables (employment, spatial employment and incentives), in county i, in year t;
a, a common intercept,
δ is the matrix of coefficients for the value of lagged endogenous variables (employment, spatial employment and MBDP incentives);
Ζi,t-n is the lagged endogenous variables (at four lags as per AIC)
The β matrix are the coefficients for the trend and quarterly dummies;
εt the error term where we assume εt → iid N(ο,σ).
Summary statistics appear in Graphic 2 below.
Graphic 2: Summary Statistics 2012:Q1-2016:Q4
| Mean | Median | Maximum | Minimum | Std. Dev. | |
| Approved MBDP Incentives ($2016) | 145,933.6 | 0 | 14,830,668 | 0 | 771,839.4 |
| Disbursed MBDP Incentives ($2016) | 77,808.05 | 0 | 10,278,331 | 0 | 516,696 |
| Total Employment | 49,176.03 | 11,742 | 759,508 | 252 | 11,9791.1 |
| Manufacturing Employment | 6,958.076 | 2,039 | 88,683 | 3 | 14,921.13 |
| Spatial Total Employment | 51,207.77 | 16,686 | 384,867 | 1,779.75 | 77,151.09 |
| Spatial Manufacturing Employment | 6,997.29 | 2,100 | 42,025 | 26.5 | 9,611.202 |
| (N=1660, with 83 cross section) |
Evaluating the effect of incentives offers several challenges to an econometrician. We cannot know, a priori, for example, the exact timing of the resulting start of new hires or time of when actual construction on a new project occurs at a particular location. We also must be concerned with the possibility that the incentives are going to firms who are choosing more favorable or less favorable places to locate. If the choices aren’t random, this risks some bias in the estimated impact. This is known as endogeneity bias, and is a problem that plagues research on incentives of all kinds.
To address this, we propose a very flexible model that allows the impact to materialize at different speeds. We also favor this model since it allows us to test endogeneity, with very few assumptions. We include a spatial component for most estimates for the very understandable reason that labor markets cross county borders.
Finally, we report the impulse response function rather than focus on the statistical model for two reasons. First, the accumulated lagged impacts in the estimation output are difficult to interpret without additional computations. The additional computations are the IRF, which we will illustrate. Second, the IRF is an appealing visualization of the estimated effects of these incentives on employment, which was a stated goal of the policy. These IRFs provide us a simulation of a large shock (typically one standard deviation) of the incentive on employment. Thus, the IRF tells us the cumulative effect of the MBDP incentive on employment, both annually and cumulatively over time.
The spatial PVAR offers the same approach of traditional time series-cross sectional models (e.g. Hicks and LaFaive, 2011), while allowing less restrictive assumptions regarding the timing of impacts.
[*] These data are available here: https://ledextract.ces.census.gov
[†] Total employment, manufacturing employment, spatial values of each and the MBDP funding all fail a unit root test at the 0.001 level. (Levin, Lin and Chu, 2002). Nonstationary variables are those which exhibit a time trend and will thus possess a spurious correlation due to observation over time.
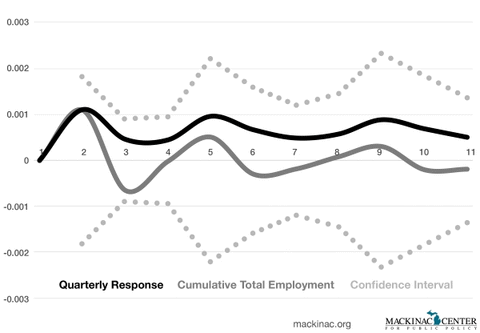
Graphic 3 illustrates the cumulative impulse response function of total employment to disbursed MBDP funds as estimated in equation 1 above.
Graphic 3: IRF of Total Employment to One Standard Deviation Change in Disbursed MBDP Incentives
This IRF is calculated from the PVAR in equation one, and we report only the effect of a one standard deviation change in inflation-adjusted disbursed MBDP funds on total employment in each county. The confidence intervals were estimated using bootstrap sampling (100 iterations). As is apparent in this graphic, the confidence interval for the MBDP impact on jobs is both above and below zero, suggesting that the impact of the program is indistinguishable from zero.
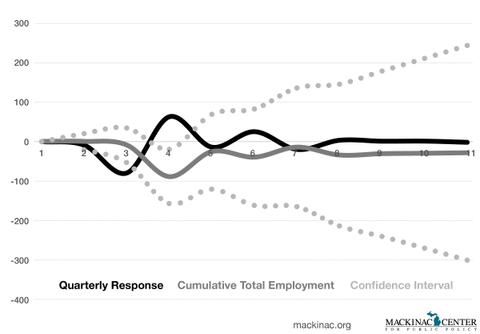
We also considered an alternative specification using a log/log transformation prior to first differencing (Arnade and Gehlar, 2005; Malone and Lusk, 2016 ). This estimate provides a similar result, with responses not statistically or economically different from zero.
Graphic 4: IRF with Log/Log Specification
The total employment effects represent the bulk of the policy analysis. However, most of the MBDP dollars are allocated to manufacturing firms. Thus, estimating the impact of these investments on manufacturing might identify better sectoral effect of these investments. In the following IRF, we illustrate both the quarterly and cumulative effects.
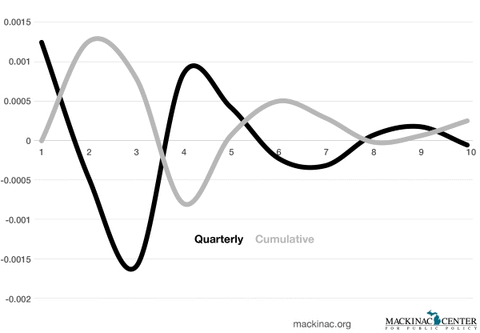
Graphic 5: Cumulative IRF of Manufacturing Employment to One Standard Deviation Change in Disbursed MBDP Incentives
We find no statistically meaningful effect of MBDP disbursement on manufacturing employment. However, we are interested in evaluating alternative specifications using a log/log transformation prior to first differencing (Arnade and Gehlar, 2005; Malone and Lusk, 2016). This estimate provides a similar result, with responses not statistically or economically different from zero. Note, that we do not include the confidence intervals here, since they are so large relative to the point estimates they obscure any variation.
Graphic 6: IRF in Log/Log Specification of Manufacturing Employment
Together, these impulse response functions provide evidence of the effect of the MBDP loan and grant programs on job creation in Michigan counties.
The MBDP program reports through fiscal 2016 roughly $156.7 million was disbursed to create 17,913 jobs, or roughly $8,747 per job. Our estimates of the impact on manufacturing show no statistically significant impact. However, the effects on total employment are negative. This implies that the MBDP program is having no effect on total or manufacturing employment.
As a robustness test we relax the Bayesian approach to ordering impacts, allowing total employment changes to influence MBDP incentives. Roughly the same result ensued for total employment, with near zero point estimates on the effect of a one standard deviation change of total employment on the incentive allocation to a county. The same results held with manufacturing employment. Also, altering the lag length to four or eight quarters likewise had no meaningful effect on the point estimates or the confidence intervals.
Together these results suggest the MBDP program of grants and loans (disbursed values only) play no role in job creation in Michigan counties where they were deployed. The only robust caveat to this conclusion is that the materialization of the impacts is longer than the five-year period under observation. That however seems unlikely given the reporting results of MBDP.
One other estimation is necessitated by these observations and one of the reviewed papers above. Gabe and Kraybill (2002) report that business optimism played a part in incentive payments in Ohio during the early 1990s. For the MBDP we evaluate whether or not the expected job created reported by businesses plays a role in the decision to fund an individual business. We find that it does.
In a simple ordinary least square model, estimating the percent of overestimate of job creation from the initial application, on the logarithm of the approved dollars is very statistically and economically meaningful.[*] Each 10-percent increase in “overestimated jobs” results in a 7-percent increase in approved MBDP funds. This result mimics those of Gabe and Kraybill (2002) and suggest that businesses that provide more optimistic estimates of job creation enjoy a higher level of approved funding. See Graphic 7 below.
Graphic 7: Percent Job Overestimate and Approved MBDP Dollars
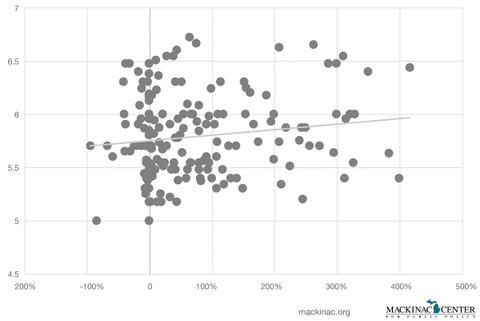
[*] F = 12.44 (p=0.001), B = 0.07, with Huber White standard errors of 0.011 (p-value=0.001).
The authors would like to thank the following people for their assistance in the production of this study. Any errors within are those of the authors.
(Note: Guerrant, Robach and DiVirgilio deserve special mention. Author Michael LaFaive has made many requests of these MEDC employees over the years and has always encountered professional, cheerful, timely — sometimes even witty — responses from them.)