
Since 2008 the Mackinac Center for Public Policy — and more recently in conjunction with the Washington, D.C.-based Tax Foundation — has worked to estimate the degree to which cigarettes are smuggled into and out of American states. Our research, and that of other scholars too, suggests that smuggling is a rampant problem, particularly in states with high cigarette excise taxes.
Unintended and unforeseen consequences are a frequent problem in public policy. Few politicians realize when they vote for higher excise taxes that doing so may dramatically increase cigarette-related crime, such as smuggling. These crimes not only deprive local and state governments of tax revenues, they also tend to descend into violence, which produces all sorts of unnecessary damage. Policymakers should take these realities into consideration when contemplating how much to tax cigarettes.
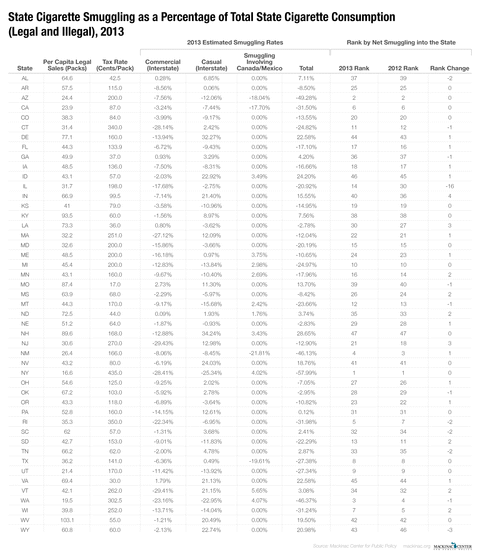
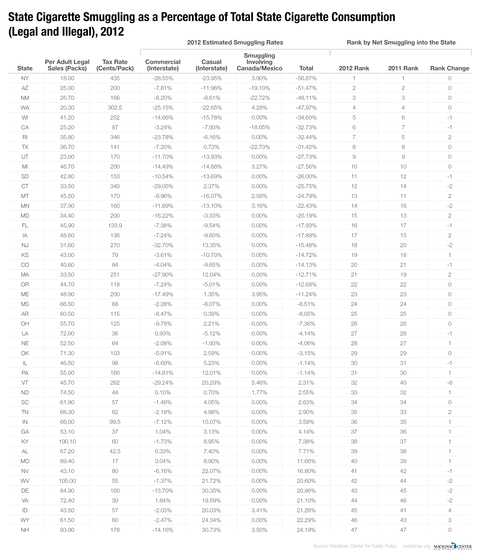
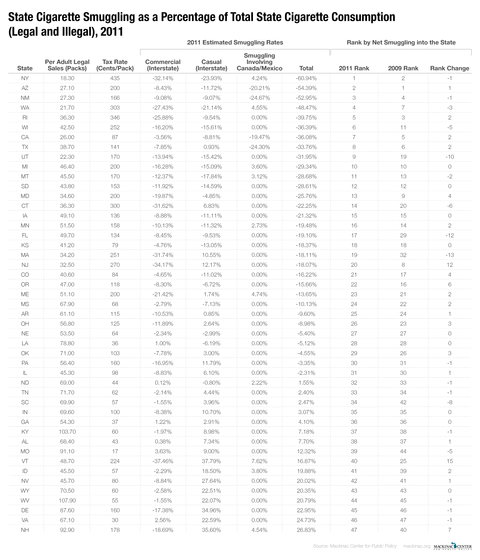
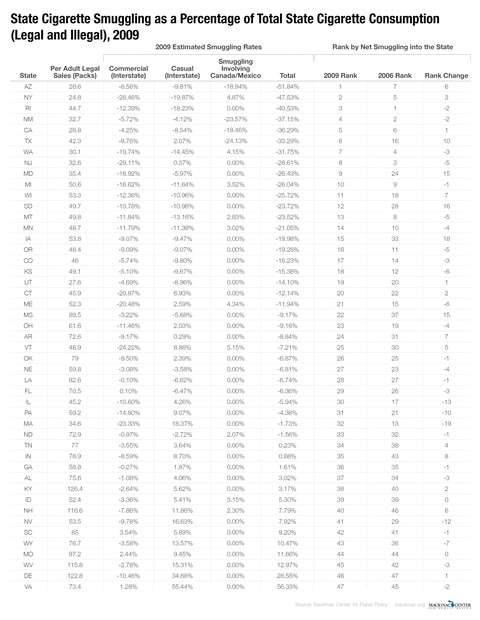
This report analyzes the relationship between cigarette tax rates and cigarette smuggling rates. It relies on the same statistical model used in our previous studies, but uses the latest available data from 2014. New York State once again claims the highest smuggling rate in the nation. In fact, according to our analysis, New Yorkers consume more smuggled cigarettes than they do legally taxed ones. New York state has the highest excise tax rate on cigarettes in the country at $4.35 per pack and New York City adds another $1.50 tax. Arizona, Washington state, New Mexico and Minnesota round out the top five states for percentage of in-bound smuggling. Michigan ranks 12th, down two positions.
Massachusetts distinguished itself between our 2015 and 2016 analyses for its change in rank among smuggling states. It leapt 15 positions from 22nd in our rankings to 7th. Minnesota increased by 11 spots from 16th to 5th and we expect to see the North Star State continue to climb due to a state law that ties automatic cigarette tax increases to inflation.
The top cigarette export state was New Hampshire. For every 100 cigarettes consumed there, an additional 81 were smuggled out and likely ended up being consumed by smokers in neighboring states. Idaho, Virginia, Delaware and Wyoming follow New Hampshire with the highest export smuggling rates.
In addition to providing the details about this analysis of new data, this study also provides a thorough review of the literature on this topic. There has been a lot of research conducted on this question, by academics and published in scholarly journals, but also by government agencies and other think tanks. The research that has been published over the past 11 years on cigarette smuggling is described in this study.
These studies use different methodologies and datasets and come to somewhat different conclusions about the specific smuggling rates of jurisdictions in the U.S. But almost all suggest that cigarette smuggling is a significant problem, generally aligning with our findings.
The Mackinac Center first took a focused interest in cigarette smuggling in 2002 when one of its scholars — James Damask — published a short essay about men who had been arrested for reselling in Michigan large amounts of cigarettes originally purchased in North Carolina. Those arrests revealed that a portion of their smuggling profits were being used to assist the Hezbollah, a group officially designated as a terrorist organization by the U.S. government.[1]
Subsequent anecdotal evidence about smuggling in Michigan and elsewhere led us to explore a full study of the relationship between cigarette tax rates and smuggling rates, including estimates for each state’s rate of smuggling. The study, released in 2008 and using data from 2006, included a statistical model to measure two types of smuggling: casual and commercial. Casual smuggling involves individuals who cross into another state or taxing jurisdiction to acquire cigarettes at a lower cost, typically for personal consumption. Commercial smuggling involves larger, long-haul shipments of cigarettes, say a van or semi-tractor trailer moving cigarettes from North Carolina to Maryland or Michigan. We published updates to this analysis in 2010, 2013, 2014, 2015 and now 2016.
One of the challenges of designing a statistical model to analyze the impact of cigarette taxes on smuggling rates is determining what to count as smuggled. Not all tax avoidance is tax evasion and states differ in how they define smuggled goods. Some states, such as Minnesota, tolerate a modicum of cross-border cigarette shopping. For instance, it wouldn’t necessarily be illegal in these states to purchase cigarettes for your own personal consumption in a neighboring state and then bring them back across the border to be consumed in your home state. States like Michigan, on the other hand, do not tolerate any cross-border shopping and maintains a zero tolerance policy. Possessing one single cigarette stick in Michigan brought in from another state is illegal.[2]
It is impossible for scholars to know what percentage of cigarettes brought in from one state to another falls under the legal limit (one carton per month, for example) and the amount brought in that exceeds it. Some scholars identify the total as “diversion” or both “tax evasion and avoidance.” Our statistical model attempts to capture both casual smuggling and commercial smuggling.
The statistical model employed in this study is a residual model, designed to compare the published smoking rates of adults in 47 states with legal paid sales of cigarettes.[*] The difference between the amount of cigarettes that are being smoked in the state and what are acquired through legal sales could be explained by some form of smuggling, and this is our assumption. The model also takes into consideration a variety of factors that might impact casual and commercial smuggling, such as proximity to a low-tax state, border county populations and presence of Native American reservations.
A complete description of the model and assumptions can be found in the appendix to this study.
[*] “North Carolina is excluded from our estimate because it is the source state for our “commercial smuggling” calculations. Hawaii and Alaska were excluded due to the challenges of modeling states that are noncontiguous.
There have been a significant number of new empirical, academic studies on the subject of cigarette smuggling that have been published in different scholarly journals and by think tanks, government agencies and others over the last several years.
These papers almost universally recognize that a significant amount of cigarette smuggling takes place in North America, though estimates differ due in large part to methodology, time periods of study and data availability. The following section briefly describes these studies and their findings.[*] They appear in reverse chronological order.
IHS Global, Inc. published “Cigarette Purchases by New York Consumers from Tribal Retailers in New York State” earlier this year. The study notes that there were approximately 761 million packs of cigarettes consumed in New York State in 2015. State tax revenues for that year suggest, however, that taxes were paid on only 289 million packs (38 percent).[3] The difference between the two figures — what the authors call a “shortfall” — suggests a smuggling rate of 62 percent in the Empire State.[†]
“Understanding the U.S. Illicit Tobacco Market: Characteristics, Policy Context, and Lessons from International Experiences” is a large study published by the National Research Council and Institute of Medicine in 2015. The report estimates that America’s illicit cigarette market ranges between 8.5 percent of “consumption subject to tax avoidance and evasion” and 21 percent of the total. The lower bound is a calculation made by the authors, while the higher bound comes from “plausible estimates” of another research paper that we describe in more detail below.[4]
The authors of the report used figures from one of our previously published studies to calculate the national tax avoidance, or smuggling, rate in 2012 and estimate it was 13.5 percent.[5] We ran a statistical analysis of the two studies’ state-by-state smuggling estimates last year. We found that the correlation coefficient between the smuggling estimates from the two studies is 0.63. This suggests that the estimates are quite similar.[‡]
Also published in 2015 was a paper titled “Reservation Prices: An Economic Analysis of Cigarette Purchases on Indian Reservations.” The paper was not designed to measure smuggling rates per se but rather the “economic incidence of the tax break” provided on cigarette purchases on Indian reservations. The authors also try to assess whether or not that tax break increased or decreased consumers’ demand for lower quality cigarettes. It did, however, provided insight into one component of New York State’s overall smuggling rate.
The dataset used in the study runs from 2003 through 2009 and comes from the New York State Adult Tobacco Survey, conducted by the New York State Department of Health. The authors used 6,539 current smokers in their sample. Some 19 percent said that they always purchase their cigarettes on reservations, a form of casual smuggling.[6]
Several government agencies in other states have attempted to estimate cigarette smuggling rates in recent years. The State of California’s Board of Equalization concludes in “Revenue Estimate: Cigarette and Tobacco Products Tax Evasion” that 16 percent of the cigarettes consumed in the Golden State in 2013 were not taxed. The figures are estimated based on a unique statistical model created for this paper that was published in 2014.[7]
Also in 2014, the Wisconsin Department of Revenue sought answers to similar questions studied by the California Board of Equalization. They published “Study of Wisconsin’s Cigarette Tax Collection System,” which forecasts a tax evasion rate of between 5.8 percent and 7.7 percent in Wisconsin for 2015. The “cigarette tax gap” estimates used in the study calculated the difference between actual consumption and excise tax revenue and what excise tax revenue should be based on per-capita adult smoking rates. The difference in revenues represents the level of tax evasion.[8]
The Commission on Illegal Tobacco in Massachusetts also analyzed cigarette smuggling in 2014. Its report indicated that economists at the Massachusetts Department of Revenue believed that between 7 and 20 percent of the total market for cigarettes in the state in 2012 were smuggled. These economists also predicted an increase in the smuggling rate to between 8.3 percent and 27.5 percent after the state’s $1.00 excise tax increase took effect on July 31, 2013. According to the Commission, revenue officials made these estimations by comparing “national consumption estimates … to the state’s taxed sales data and literature.”[9]
The Department of Revenue in Washington state also published a paper on this topic in 2014, titled “Cigarette Tax Evasion Estimate - FY 2013.” The estimated smuggling rate is pegged at nearly one third of the entire cigarette market — both legal and illegal sales. The estimate is derived by comparing per-capita cigarette consumption with per-capita sales of cigarettes. The estimate excludes, rather than controls for, the possible contributions of smuggled, but legally untaxed, cigarettes from Indian reservations in the state.[10]
Two studies were published in 2014 that looked at the cigarette smuggling rates in Ontario, Canada. The Ontario Convenience Stores Association contracted with NIRIC, a business research consultancy, and published “OCSA Contraband Tobacco Ontario Study September & October 2014.” It was an analysis of discarded cigarette butts from 130 locations throughout Ontario. Some of discarded butts were of foreign or Native American origin and others were unbranded. On average, they estimated that 22.5 percent of all discarded cigarette packs across these locations were contraband.[11]
The National Coalition Against Contraband Tobacco also conducted a survey of adult smokers in Ontario from October 2013 to July 2014. This online survey found that between 22 percent and 42 percent of cigarette products purchased by respondents were illicit.[12]
Published in the journal Tobacco Control in 2014, a group of scholars used a rather unique research method to estimate rates of cigarette smuggling throughout the entire country. The article, “A Novel Approach to Estimating the Prevalence of Untaxed Cigarettes in the USA,” describes the results of a project that invited smokers to mail the researchers an unopened pack of their usual brand of cigarettes in 2009 and 2010. Smokers who did were paid $25. The authors found that 20 percent of the packs returned to them in 2009 lacked a tax stamp from the state where the survey participant lived and 21 percent did in 2010. They also noticed that “the prevalence of untaxed cigarettes was higher in states with higher-excise taxes.”[13]
Tobacco Control also published “Cigarette Trafficking in Five Northeastern US Cities” in 2013. The authors of the study collected and examined discarded cigarette packages in Boston, New York City, Philadelphia, Providence, Rhode Island and the District of Columbia. By looking at each package, the researchers identified tax stamps which should identify the location from which the cigarettes originated. They determined that 58.7 percent of the 1,439 littered cigarette packs they collected did not have a proper local tax stamp and between 30.5 and 42.1 percent could be attributed to illegal trafficking. The authors also estimate that these cities lose between $680 million and $729 million in combined tax revenue as a result of this smuggling.[14]
Of the city-specific numbers generated by the authors’ research, two stand out. More than 75 percent of the discarded packs with a nonlocal stamp collected in Providence came from Massachusetts. Massachusetts itself maintains a tax rate of $2.51 per pack, but Rhode Island’s rate is even higher at $3.75 per pack. Of those collected in the District of Columbia, 50 percent originated in Virginia and 32 percent in Maryland.[15]
Another city-specific analysis was published in Tobacco Control in 2013. The article, titled “The Illegal Cigarette Market in a Socioeconomically Deprived Inner-City Area: The Case of the South Bronx,” describes the results of a discarded cigarette pack analysis. Researchers found that “76.2 percent of cigarette packs collected avoided the combined New York City and State tax.” Almost 58 percent were not taxed at all. The authors’ conclusion was that poor areas of the U.S. may have higher tax evasion and avoidance rates than elsewhere in the country.[16]
These findings appear to lineup with another city-specific research effort that was conducted by the New York City Department of Finance during 2014. The finance department conducted an “administrative inspection” of 322 cigarette retailers within the city. They report that 191 inspections, or 59 percent, “resulted in some sort of illegal cigarette(s) seized.”[17]
Andrew Chang & Company, LLC wrote “The State and Local Impact of Tobacco Prices on Smuggling and Black Market Tobacco Sales” for the California Foundation for Commerce & Education and released it in September 2013. This report focused on California and used data from 2001 through 2010. The authors pegged California’s 2010 smuggling rate at almost 19 percent of the total market. Their conclusion is based on a residual model, comparing the difference between taxed legal sales and an estimate of consumption.[18]
In 2012, the business consultancy John Dunham and Associates released “An Examination of Cigarette Sales in New York State by Source: 2011” for the New York Association of Convenience Stores. The report concludes that 52 percent of cigarettes in the Empire State came from “alternative sources including lower taxed states, Native American reservations, military sales or duty free sales.” This figure does not include cigarettes that were smuggled into the state from international sources.[19]
The National Tax Journal published a paper in 2011 that looked at cigarette tax evasion rates in New York City. The authors of the article, titled “Using Littered Pack Data to Estimate Cigarette Tax Avoidance in New York City,” collected discarded packs in 30 city census tracts before a 2008 state excise tax increase of $1.25 and then three times afterward. They found that 15 percent of discarded packs had no tax stamp before the state excise tax took effect, but that number leapt to 24 percent afterward.[20]
A 2010 National Bureau of Economic Research working paper called “Excise Tax Avoidance: The Case of State Cigarette Taxes” uses data from two supplements to the U.S. Current Population Survey in 2003 and 2006-2007 that asked participants about tobacco use and tax avoidance. The researchers used these results to estimate cross-border purchasing rates for cigarette consumers in each state, with Vermont and the District of Columbia topping the table at 18.7 percent and 18.5 percent, respectively. Florida, Hawaii, Kentucky, Mississippi, Missouri, Nevada, North Dakota, and South Carolina all had cross-border purchasing rates of less than 1 percent and New York state’s rate was only 4.1 percent.[21]
The authors of the paper note that their “calculations suggest that many states already impose cigarette excise taxes that are higher than optimal.” They also point out that their “empirical results suggest that the tax avoidance increases with income” and “state cigarette taxes may be even more regressive than commonly estimated.”[22]
A 2010 study analyzed discarded cigarette packs in Chicago and surrounding areas with different cigarette tax rates in 2007. According to the study’s author, economist David Merriman, 29 percent of all the packs collected in the city bore the tax stamp of Indiana. Merriman also reports in “The Micro-Geography of Tax Avoidance: Evidence from Littered Cigarette Packs in Chicago” that only 36 percent of those discarded cigarette packages collected bore the tax stamps of Cook County and only 25 percent had the tax stamp from the city of Chicago.[§] In other words, as Merriman points out, “Chicago littered packs were slightly more likely to have an Indiana stamp than a Chicago stamp.”[23]
“Cigarette Tax Evasion in Minnesota” was prepared by economist Marsha Blumenthal in 2009 for the Minnesota Department of Revenue. It reported several conceivable statewide smuggling rates based on survey research and estimated a 2 percent to 8 percent smuggling rate in Minnesota based on tax gaps between what should have been collected in excise tax revenue and what was actually collected.[24]
Another study published in 2009 discusses the global impact of the illegal market in cigarettes around the world and concludes that “if the global illicit trade were eliminated, governments would gain at least $31 billion in additional tax revenue, and from 2030 onwards, would save over 160,000 lives a year.” The report ranks the United States as the third highest in the world in 2007 for the illicit trade in cigarettes, behind Russia and China.[25]
An award-winning study in 2008 estimated that between 13 percent and 25 percent of consumers nationwide purchase their cigarettes in “border localities,” such as over a state border or on an American Indian reservation. The datasets used for this paper end in 2002 and rely on consumers who live in Metropolitan Statistical Areas rather than entire states. “How Far to the Border: The Extent and Impact of Cross-Border Casual Cigarette Smuggling” was selected for the Richard Musgrave Prize by the National Tax Association for “authors of outstanding new contributions in the field” of public finance.[26]
The highest casual smuggling rate in this paper was the District of Columbia at 63.5 percent of total consumers. The lowest was California at a tiny 0.01 percent. New York — today a perennial leader in overall smuggling — had a rate of 19.6 percent. The author, economist Michael Lovenheim, concludes, “The central implication of this study is cross-border smuggling confounds many of the potential health and revenue gains from cigarette taxation.”[**]
A 2008 study also tried to measure the impact of casual smuggling nationwide. “Crossing the Line: Direct Estimation of Cross-Border Cigarette Sales and the Effect on Tax Revenue” estimates the degree to which consumers smuggle cigarettes for personal consumption. They conclude that “an individual is willing to travel 3 miles to save one dollar on a pack of cigarettes,” but that nationwide the casual smuggling rate for consumers is only 4 percent.[27]
“Washington State Cigarette Consumption Revisited” employs an econometric model using eight years of data, from 1997 to 2004. Published in 2007, the authors find that Washington’s average smuggling rate — or nontaxed sales — was 14.9 percent. They provided estimates for all 50 states and the District of Columbia and found Massachusetts to have the highest smuggling rate of 17 percent. The U.S. average rate was 1.7 percent.[28]
An oft-cited paper by economist Mark Stehr, “Cigarette Tax Avoidance and Evasion,” estimates that between 68 percent and 85 percent of changes to legal paid sales may be explained by tax avoidance and evasion.[††] Stehr also estimated that, of the states in his analysis, some 12.7 percent of cigarettes were being purchased without payment of state taxes by 2001.[29]
Finally, a 2005 paper examines 2001 survey data taken from 3,602 smokers in the United States and determined that 34 percent of respondents “regularly purchase from a low or untaxed venue.” A “venue” could mean an Indian reservation or other state or country. Of the 214 respondents surveyed from Binghamton/Johnson City, New York, 66 percent reported purchasing lower priced smokes in a different state, presumably in Pennsylvania, which is less than 20 miles away.[30]
[*]Several older papers listed below appeared in both the 2008 and 2010 Mackinac Center studies but we choose to repeat them here and for two reasons: 1) they represent part of the original literature review we conducted before building our own statistical model and 2) the scale and quality of these works are such that leaving them out would diminish the usefulness of this report.
[†]Similar to our approach, the authors primarily arrive at NY’s consumption figure largely based on the CDC’s smoking prevalence figure. However, they arrive at the final number based on the NY population and US total consumption. They then take their estimated total consumption and subtract from it legal sales to get the shortfall. Our model starts with legal sales by state and determine what share of each state's legal sales per capita are explained by prevalence figures and time trend to determine the shortfall, or “residual.”
[‡]There were some notable dissimilarities, especially at the extremes. For instance, the Institute of Medicine’s study estimates that Delaware, New Hampshire and South Carolina have cigarette-exporting rates exceeding 70 percent. The Mackinac Center’s 2014 study using 2012 data found export rates for those states of 24.4 percent, 28.3 percent and 2.3 percent, respectively. Conversely, the Institute of Medicine estimated a smuggling rate for Maryland of just 0.89 percent of consumption while the Center’s estimate exceeded 24 percent. Peter Reuter and Malay Majmundar, eds.,
[§]These discarded packages were collected before the most recent cigarette excise tax increases by all three units of government. Cook County raised their excise tax $1.00 in 2013 to $3.00 per pack and the city of Chicago raised its excise tax by 50 cents in 2014. Moreover, Chicago is not the only city within Cook County that imposes a cigarette excise tax. Both Evanston and Cicero impose excise taxes on cigarettes of 50 cents and 16 cents, respectively. “Cook County Department of Revenue Tobacco Tax Ordinance” (Cook County Department of Revenue, 2013), https://perma.cc
[**]Michael Lovenheim, “How Far to the Border?: The Extent and Impact of Cross-Border Casual Cigarette Smuggling,” National Tax Journal LXI, no. 1 (March 2008), https://perma.cc/9HY9-RHWN. Along these lines, a 2014 study titled “Do Higher Tobacco Taxes Reduce Adult Smoking? New Evidence of the Effect of Recent Cigarette Tax Increases on Adult Smoking” in Economic Inquiry last year examines the degree to which recent excise tax increases impact adult smoking rates. The authors found very little evidence that higher tax rates lead to fewer smokers. The likely reason is that taxes are already so high that those who remain smokers have a “strong preferences” for doing so. The authors write: “Considering all the evidence, we conclude that there is insufficient justification for the widespread belief that raising cigarette taxes will significantly reduce cigarette consumption among adults, even young adults.” Kevin Callison and Robert Kaestner, “Do Higher Tobacco Taxes Reduce Adult Smoking? New Evidence of the Effect of Recent Cigarette Tax Increases on Adult Smoking,” Economic Inquiry 52, no. 1 (2014): 157, https://perma.cc
[††]Related, a 1995 study by economist R. Morris Coats found that about 80 percent of the “tax effect” on cigarette sales are due to cross-border purchases and the rest from a decline in consumption. R. Morris Coats, “A Note on Estimating Cross-Border Effects of State Cigarette Taxes,” National Tax Journal XLVIII, no. 4 (1995): 573–584, https://perma.cc
As evidenced from the studies just described, there are a number of different ways that researchers have attempted to estimate cigarette smuggling rates. The research design, data sources and type of statistical analysis employed all impact these estimates.
While some of the estimates cited above differ from our previous analyses and the most recent results that are described below, many of them do roughly line up with our results. While there’s no “right” estimate, it’s encouraging to see that many of the analyses that have been conducted typically come to similar conclusions. Cigarette smuggling — inspired by tax evasion or avoidance — is a significant problem in many areas of the country.
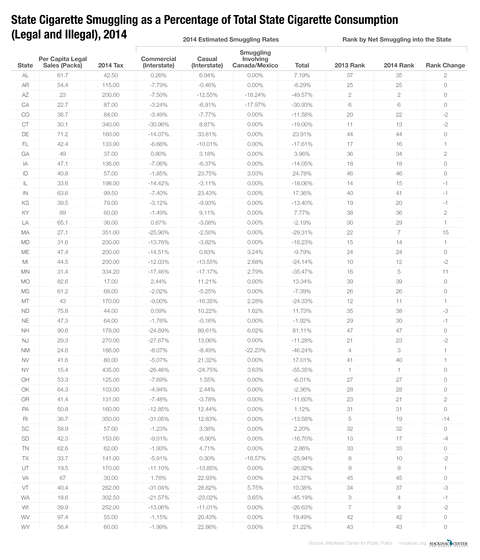
Our most recent estimates, using the latest available data at the time of this written — through 2014 — find the states with the highest inbound smuggling rates are New York (55.4 percent), Arizona (49.6 percent), New Mexico (46.2 percent), Washington (45.2 percent), Minnesota (35.5 percent), California (30.9 percent), Massachusetts (29.3 percent), Utah (26.8 percent), Wisconsin (26.6 percent) and Texas (25.9 percent).
The state of New York has been a perennial number one in our rankings. Its high state excise tax rate of $4.35 per pack combined with New York City’s $1.50 tax per pack and its proximity to lower taxed states (Pennsylvania and Virginia, for example) all contribute to its high smuggling rate. But Arizona and New Mexico are not far behind, both with smuggling rates within 10 percentage points of New York’s.
There is an important point worth discussing concerning the smuggling rates in Arizona and New Mexico. The statistical model used in this analysis contains an international component which attributes a certain amount of smuggling from Mexico or to Canada. Based on discussions with law enforcement, we have come to believe that some percentage of illicit cigarette trafficking that the model attributes solely to being smuggled in from Mexico may in fact be passing through bonded warehouses, having entered the United States from some other country.
A bonded warehouse is a way station of sorts where international goods are processed before being dispatched within the United States. It is all too easy — we are told — for some percentage of international cigarette shipments that land in bonded warehouses to get diverted for smuggling purposes. We believe our overall smuggling rate is accurate, but based on this information, it is possible that the percentage of smuggling from Mexico to Arizona (18.2 percent) and New Mexico (22.2 percent) is overstated. The same could be said for California and Texas, which our model attributes 18 percent and 19 percent of illicit traffic coming from Mexico, respectively.
Through 2014 the states with the highest net outbound smuggling export rates are New Hampshire (81.1 percent), Idaho (24.8 percent), Virginia (24.4 percent), Delaware (23.9 percent), Wyoming (21.2 percent), West Virginia (19.5 percent), Indiana (17.4 percent), Nevada (17.0 percent), Missouri (13.3 percent) and North Dakota (11.7 percent).
New Hampshire clearly stands alone in terms of outbound smuggling, according to this analysis. This may be surprising, because it levies a relatively hefty $1.78 excise tax on packs of cigarettes. Its status, however, as cigarette export king is likely a function of being sandwiched between Vermont with its $3.08 tax per pack and Maine with its $2.00 tax per pack. In addition, Canada, directly to the North, imports a small percentage of New Hampshire smokes too. Our model takes smuggling into Canada into account and incorporates those exports from a state’s overall smuggling rate. We estimate that for every 100 cigarettes consumed in New Hampshire an additional six are smuggled into Canada.
The states in our study with the biggest year-over-year upward moves by rank are Massachusetts and Minnesota which leapt 15 and 11 spots — Massachusetts is now 14th and Minnesota fifth. Both states enacted large state excise tax increases in 2013 by $1.00 and $1.60, respectively, and so their climb up the rankings is not surprising.[31]
Minnesota has actually raised its cigarette taxes again in 2015 by 7 cents and the again by 10 cents earlier this year.[32] The North Star State adopted a law to facilitate automatic cigarette tax increases based on inflation in 2013, which we expect will put constant upward pressure on smuggling and other unintended consequences. Minnesota’s neighbor, North Dakota, maintains an excise tax rate of only 44 cents.[33] The tax differential between these two states probably goes a long way in explaining North Dakota’s top-10 cigarette export rate of 11.7 percent.
The biggest notable drop in rankings was from Rhode Island, which saw its rank drop from fifth in the nation in 2013 to 19th in 2014. The likely reason for the drop was not due to its own efforts, but instead to the $1.00 cigarette tax increase in Massachusetts. With higher excise taxes in a neighboring states, Rhode Islander’s had one less attractive option for acquiring less expensive cigarettes.
The table below shows the full results of our statistical analysis.
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
In our 2008 report, we zeroed in on the influence of excise tax increases at the county level, using a proprietary dataset of cigarette sales obtained by a large Midwestern wholesaler. This micro-level data and our analysis served as a robustness check on both the theoretical underpinnings of our larger, state-level statistical model. This county-level analysis also helped us shed light on the nature of casual smuggling — low-level tax avoidance through the cross-border purchasing and transporting of cigarettes for personal consumption from a lower taxed state or other taxing jurisdiction.
The wholesaler data ran from January 2006 through September 2008, during which time two of Michigan’s neighboring states — Indiana and Wisconsin — raised their cigarette excise taxes. This allowed us to peer into the purchasing decisions of Michigan retailers in counties bordering those states. Indiana raises its excise tax 79 percent, from 55.5 cents per pack to 99.5 cents in July 2007. In January 2008 Wisconsin’s excise tax climbed by 130 percent, from 77 cents per pack to $1.77.[34]
Economic theory suggests that smokers in Michigan would buy more cigarettes from in-state retailers when excise taxes on cigarettes are raised by legislators in neighboring states. The reason for this is that the relative benefit of crossing into nearby states to buy cigarettes declines as the tax-induced price of cigarettes in those states rises. This makes shopping closer to home a more cost-effective alternative.
The data bore out the theory. Sales of cigarettes from the large wholesaler to Michigan retailers in counties bordering Indiana in the three months leading up to the Hoosier excise tax hike taking effect leapt by 58 percent. Retailers were clearly stocking up for what they predicted would be an increase in sales on their side of the Michigan-Indiana border. The higher sales were generally maintained after the hike took effect too, running 53 percent higher than they had before the adoption of a cigarette excise tax increase in Indiana.[35]
The sales response to excise tax hikes was smaller in Michigan counties bordering Wisconsin. Sales to Michigan retailers only increased by 8 percent. We speculate that this was partly a function of the relatively smaller populations in Michigan-Wisconsin border counties — they are all in the western part of Michigan’s sparsely populated Upper Peninsula.
So far, we’ve discussed the results of our statistical model concerning the relationship between cigarette tax rates and illicit smuggling. The figures this analysis produces are important for policymakers to consider when debating the merits of making changes to cigarette tax rates. But, as with any statistical analysis, its reflection of reality is limited to the quality of the data it uses and to the appropriateness and accuracy of its assumptions.
Recognizing this, we would also like to present some evidence that suggests that cigarette smuggling is, in fact, a real issue that impacts real people. Although these are anecdotes, they imply that smuggling and related crimes are becoming more common in the United States as more states have increased cigarette taxes. They also reveal other costs to cigarette smuggling — the corruption, violence and required policing associated with this illegal activity. Policymakers should also keep these stories in mind when considering cigarette tax rates.
We expect these types of stories to continue. There seems to be a steady interest in raising cigarette taxes in state legislatures, usually under the assumption that doing so will raise more revenue for the government and reduce smoking. The unintended consequences of these policies matter though and can be costly.
The purpose of our statistical analysis and related discussion on the relationship between cigarette taxes rates and illicit smuggling activity is not to determine optimal tax rates for states. Instead, we hope this report encourages policymakers and the public to consider the often unseen costs of raising cigarette taxes, such as increasing the profits of smugglers and encouraging more people to partake in illegal acts. Cigarette tax hike proposals should take into consideration the impact on government through increased revenue (although revenue losses are possible), the impact on public health through reductions in smoking, and the impact on law enforcement and society through increased smuggling.
It is our recommendation that lawmakers in states that already have high excise taxes on cigarettes take a type of economic Hippocratic Oath, and, first, do no more harm. Some states may even wish to roll back cigarette tax rates and offset any revenue losses they may experience with spending cuts elsewhere. This is arguably the most effective way of addressing the smuggling problem. Other states might want to close the gap between their cigarette taxes and those in nearby states. This could mean reducing taxes for some states and raising them for others. Either way, this would reduce the reward for violating state law by decreasing arbitrage opportunities for smuggling.
There is another vital reason to reduce the degree to which states feel compelled to impose excise tax rates on cigarettes: individual liberty. Politicians the world over have singled out smokers for their “sin.” The sin taxes imposed on their products — it is argued — is good for the consumer. It raises the cost to consuming a product that has been demonstrated to be unhealthy, and it simultaneously raises revenue that can be used for a wide variety of other government initiatives.
The flip side is of course that subjecting cigarettes and other tobacco products to hefty taxes is a soft version of prohibition and a restriction of consumer choice. As we noted in a 2008 report (citations in the original):
Our focus on taxes has meant that we have not dwelled on the risks of smoking. This does not mean we think tobacco usage is harmless for consumers. Rather, we believe our findings may help remind policymakers and the public that the debate over cigarette taxes would probably benefit from more nuance and balance.
Still, in many cases the urge to raise cigarette taxes seems to involve more than a cost-benefit analysis; it appears to be driven instead by a conviction that public policy should be used to eliminate smoking altogether. This is a moral conviction and deserves more than an accountant’s ledger in response.
Smoking has been linked to serious health problems, and there is no question that heavy cigarette consumption is a risky habit. People who do not like cigarette smoking have a right to refrain from it and exclude it from their property. Yet using taxes and new laws to make citizens give up smoking in their personal lives raises important concerns about individual freedom.
Cigarette smoking is only one of many risky behaviors that people enjoy. Others include driving cars, riding horses, skydiving, overeating and casual sex. High taxes on these activities might eliminate some health risks and reduce the associated health care costs, but people do not always behave as expected. They often enjoy an activity precisely because it involves some risk. They may respond to higher costs by seeking to avoid the costs, not the activity, even when avoiding the costs is illegal. After all, that risk may become part of the attraction.
It does not take much imagination, especially after America’s experiment with alcohol prohibition, to see that fighting this impulse could generate an intrusive enforcement regime and a growing disrespect for the law. Intrusiveness and lawlessness would be more than just unpleasant: They could undermine people’s pursuit of happiness. That pursuit may sometimes be erratic and wrongheaded, but it is part of the value and purpose of life. As U.S. Supreme Court Justice George Sutherland once said, “To give a man his life, but deny him his liberty, is to take from him all that makes his life worth living.”
As a society, then, we should be careful about marking people down for harsher tax treatment because they engage in certain personal activities. When taxation moves beyond a modest revenue measure, it can become a relentless social crusade, with each unintended consequence generating new reasons for more revenue and more enforcement.
Our fellow citizens deserve better than that. No matter how much we may want a tobacco-free America, a free America is important too.[49]
Both anecdotal and empirical evidence suggest that cigarette smuggling is a significant problem. The smuggling and related unintended consequences are born of high excise tax rate differentials between states, among other factors. This study is just one contribution to analyses that have been performed by academics, think tanks, business consultants and government agencies.
The Mackinac Center’s research in this field was born from an interest in published news accounts of high excise taxes and reports of cigarette smuggling arrests. These arrests — involving a smuggling cell from North Carolina — remain among the highest profile smuggling busts in the Great Lake State.
To estimate of smuggling rates, we fed data such as legal paid sales of cigarettes and adult smoking rates from 47 of the 48 contiguous states into a statistical model of its own creation. The model is a relatively straightforward one. It compares the legal paid sales of cigarettes to smoking rates by state. The difference between the two must be explained somehow and we believe it can be explained by smuggling. Since the Mackinac Center first published its results in 2008 (based on data through 2006) it has had its figures updated five times, including this 2016 update using 2014 data.
New York continues to be the top target for smuggled cigarettes — our model suggests 55 percent of the cigarettes consumed there are smuggled in from other jurisdictions. This make intuitive sense as the Empire State has the nation’s highest cigarette tax rate and New York City also imposes its own local excise tax on top of that. In addition, it takes less than six hours to drive from low-tax Virginia to New York City, limiting transportation costs associated with illicit acquisition and distribution.
New Hampshire is America’s number one smuggled cigarette exporting state. For every 100 cigarettes consumed there, more than 80 are exported elsewhere. This is not a function of the state having an absolutely low excise tax rate, just a relative one. Surrounding state taxes are so much higher that it is cost effective for many people in neighboring states to casually smuggle their own cigarettes out of New Hampshire.
Without reform of excise taxation practices, many states will continue to see major arrests for cigarette smuggling operations and their related unintended consequences. Governments have simply made trafficking in cigarettes too profitable for criminal classes to avoid. One way to thwart the trade is to decrease its profitability by reducing excise taxes or decreasing the large disparities in cigarette tax rates among states. At the least, most states should avoid incentivizing more people to partake in illicit activity that comes with raising marginal cigarette tax rates.
Policymakers need to give these unintended consequences of cigarette taxes thought before jumping to raise these tax rates to new levels. But issues of taxation and illegal smuggling are not the only consideration. Lawmakers should also regard the value of the freedom of individual’s to take risks with their own health. As our model suggests, no matter the taxes levied on cigarettes, people are going to continue smoking, even if it requires them to partake in illegal activity.
In other words, hiking cigarette taxes may not be the policymaker’s version of a slam dunk — automatically boosting government revenue while simultaneously improving public health. Instead, hiking cigarette taxes can encourage illegal casual smuggling, raise the profit motive for professional criminals to engage in commercial smuggling, create new law enforcement and court costs and introduce new violence on the public as criminals fight over shares of the profits from a growing black market for cigarettes. While it’s impossible to pinpoint exactly what the all the effects of each new tax hike might be, these very real potential side effects need to be considered.
In this appendix, we discuss the empirical models and results used to produce the casual and commercial smuggling estimates presented in this paper. The results of this study build upon the existing literature, in which much support appears for the existence of substantial tax-induced cigarette smuggling, both casual and commercial.
Much of this literature employs empirical models of representative consumer demand, including such variables as cigarette price, tourism, income, race, religious affiliation and other demographic variables, in addition to the primary variables of interest: tax (or price) differentials; American Indian and military population; and distance from North Carolina.
The empirical method chosen here does not estimate consumer demand; rather, it follows the two-stage method proposed by LaFaive, Fleenor and Nesbit in 2008. We first estimate in-state consumption and then use the residual from that regression as a measure of smuggling. We then take that measure of smuggling (unexplained state sales) and regress it as a function of tax differentials and other commonly employed variables used to describe casual and commercial smuggling.
What follows is a brief description of the estimation procedure and a discussion of the results. A more thorough description of the empirical model can be found in Appendix A of LaFaive, Fleenor, and Nesbit’s 2008 study.[50]
Legal per-adult, tax-paid cigarette sales (hereafter per-adult sales) can be defined as the sum of in-state consumption and net smuggling, as presented in Equation 1:
PCSalesi,t = Consi,t + NetSmugi,t
where PCSales is per-adult cigarette sales,
Cons is in-state per-adult consumption,
NetSmug is the per-adult number of packs of cigarettes exported to residents of other states minus the number of packs imported by residents of the home state from other states or jurisdictions, including Indian reservations and military bases,
i is the state, and
t is the year.
Our first-stage regression equates to a naïve version of Equation 1, in that we do not control for any smuggling. Instead, we include only measures of in-state consumption on the right-hand side of the equation. If the smuggling of cigarettes is not prominent, then sales within the state will be approximately equal to in-state consumption. However, if smuggling is a prominent feature of the cigarette market, such a naïve model will fail to explain a large percentage of the variation in per-adult sales, resulting in residuals of large magnitude.
The sign and magnitude of the residuals from the estimation of the naïve model are of particular interest to us. Specifically, for low-tax states, the naïve model should systematically underpredict actual sales, as consumers from other states travel across state and international borders to purchase cigarettes there. Thus, actual sales in the low-tax state should exceed the consumption within the state, resulting in a positive residual. Similarly, the naïve model should systematically overpredict actual sales for high-tax states, resulting in a negative residual, as in-state residents choose to purchase cigarettes from nearby lower-tax states, Indian reservations, military bases or from illegal markets.
In order to estimate our naïve model of per-adult tax-paid cigarette sales, in-state per-adult consumption is characterized by Equation 2:
Consi,t = Smokei,t * Intensityi,t * Ri,t
where Smoke is the percent of the state’s adult population who are smokers (known as “smoking prevalence”),
Intensity is the average number of packs consumed during a year by the state’s smokers, and
R is a parameter between zero and one allowing for the underreporting of smoking prevalence.
State-by-state data on smoking prevalence is available from the Centers for Disease Control and Prevention through its Behavioral Risk Factor Surveillance System. Unfortunately, state-by-state data on smoking intensity is not readily available. LaFaive, Fleenor and Nesbit observe that smoking intensity at the national level declined roughly linearly from 1995 to 2006 and assume that smoking intensity does not vary significantly across states, allowing for a linear trend to capture the variation in smoking intensity through time, as indicated in Equation 3:[†]
Consi,t = Smokei,t * ƒ(Trendt)
where ƒ(Trendt) represents the above-described linear function of smoking intensity and its systemic underreporting.
We estimate our naïve model of per-adult sales using state-level data for the U.S. continental states for the period 1990-2009. North Carolina is excluded from our sample because it is modeled as the primary source of commercially smuggled cigarettes in the second stage regression.
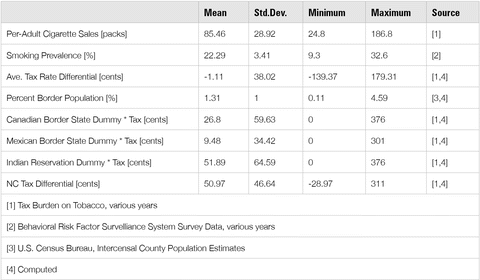
Descriptive statistics and sources for all variables used in this study can be found in Graphic 1. All dollar amounts are represented in 2009 prices.
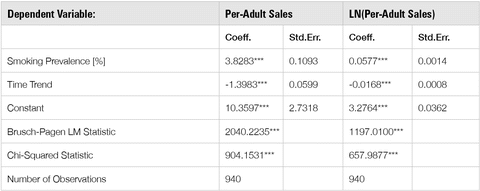
Graphic 2 presents the maximum likelihood estimates of our naïve model corrected for groupwise heteroskedasticity to allow for nonconstant variance across states. We present both linear (Columns 1 and 2) and log-linear (Columns 3 and 4) specifications for robustness, but the log-linear specification appears to more closely fit the data and hence is the preferred specification.
Per the results presented in the final two columns of Graphic 2, a 1 percentage point increase in the smoking prevalence rate results in a 5.8 percent increase in per-adult sales in the state. Furthermore, per-adult sales are shown to decrease by an average of 1.7 percent per year, which we attribute to the decline in smoking intensity over time.
Graphic 1: Descriptive Statistics and Sources of Data
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
Note: All prices are represented in constant year 2009 dollars.
Graphic 2: Maximum Likelihood Estimation: State Per-Adult Cigarette Sales, 1990-2009
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
Note: Statistical significance of 1 percent, 5 percent and 10 percent are represented by ***, ** and *, respectively. Results are corrected for groupwise heteroskedasticity via the HREG command within NLOGIT 3.0. Regressions include state fixed effects; these are withheld here for space considerations, but are available upon request.
As mentioned above, it is not the coefficient estimates from the naïve model that interest us; rather, it is the model’s residuals that are important. State with high tax rates relative to their neighbors and to North Carolina are expected to have residuals that are negative and large in magnitude, with predicted per-adult consumption exceeding the state’s observed per-adult sales, suggesting that the state’s consumers are obtaining their smokes in other jurisdictions or markets. Low-tax states are expected to have residuals that are positive and large in magnitude, with observed per-adult sales exceeding predicted per-adult consumption, suggesting that the states are net exporters of smuggled cigarettes.
We attribute most of the variation of the residual from the naïve model to the occurrence of “casual” and “commercial” smuggling. Casual smuggling can take the form of cross-border shopping between states; cross-border shopping either in Mexico or from Canada; or the purchase of untaxed cigarettes on military bases and Indian reservations by nonmilitary personnel and nontribe members. We include the weighted average tax differential — i.e., home state tax rate – weighted average border state tax rate — between the home state and the bordering states to account for tax-induced shopping across state lines. Similar to Coats’ 1995 study, the average border tax rates are weighted by county border populations.[51]
However, even with large average tax differentials, proportionally little casual smuggling is likely occur if few people live along the border relative to the state’s population. Thus, we include the population living on either side of the border divided by the home state’s total population (Percent Border Population). This percentage can take on a value greater than one when the border population in surrounding states is sufficiently large, thus causing the border population to exceed the home state’s total population. Finally, we include an interaction term between the average tax differential and percent border population.
To capture the impact of the presence of Indian reservations, we include the sum of the state excise tax and the federal excise tax rate for those states with Indian reservations. This is effectively the tax differential between the home state and the tribal land, since taxes are not generally applied to cigarettes sold on Indian lands.[‡]
Ideally, we would also like to include the tax differential with Canadian province(s) and Mexican state(s) for any U.S. states bordering Canada or Mexico. Unfortunately, accurate data on such tax rates, particularly for Mexico, were not available. Exchange rate fluctuations would further complicate the calculation of these tax differentials. As such, we simply include the sum of the home state excise tax and the federal excise tax for those states bordering either Canada or Mexico.
As described in Thursby and Thursby’s 2000 paper, commercial smuggling primarily occurs either by “diversion” or “over-the-road.”[52] Diversion involves the manipulation of accounting records, reporting only a portion of the sales.[§] Over-the-road smuggling occurs when bulk cigarettes are purchased legally in low-tax states and shipped to higher-tax states, where the cigarettes receive counterfeit stamps and enter legal markets.[**] Our empirical model controls only for over-the-road smuggling, as has been common in the literature, with the exception of Thursby and Thursby (2000).
North Carolina has generally been modeled as the primary source of commercially smuggled cigarettes, and we follow the same convention. The tax differential between the home state and North Carolina is included as our measure of commercial smuggling. Distance from North Carolina is not included in the model, since much of the previous literature suggests that transportation costs account for less than 1 percent of cigarettes’ total value. As such, transportation costs should exert a negligible impact on smuggling.[53]
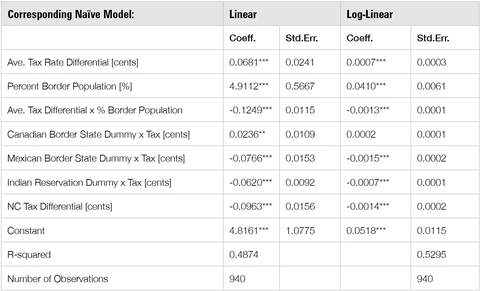
Columns 3 and 4 of Graphic provide the OLS estimation results of regressing the residuals from the log-linear naïve model against the tax differential and population variables described above. When interpreting these results, recall that the dependent variable is the actual per-adult sales minus the predicted consumption from the naïve model. This dependent variable represents net smuggling exports. Thus, a positive value of the dependent variable suggests the state is a net exporter of smuggled cigarettes, while a negative value of the dependent variable suggests the state is a net importer of smuggled cigarettes.
With the exception of the coefficient describing net smuggling to Canada, all estimates are of the correct sign and are statistically significant. An increase in the tax differential with North Carolina (our measure of commercial smuggling) is shown to reduce net smuggling out of the state, indicating an increase in commercial smuggling of cigarettes from North Carolina. States bordering Mexico or containing Indian reservations, and particularly states with larger tax rates, are shown to experience significantly increased smuggling imports from Mexico and the reservations, respectively.
The implications concerning casual smuggling are not as clear, as the coefficient of average tax rate differential is positive while the interaction term is negative. However, given the mean percent border population of 1.305, the impact of a $1 increase in the average tax differential is clearly negative, leading to a 0.161 percent reduction in net casual smuggling out of the state.[††] This is consistent with the expectation that the larger the home tax rate is relative to the average bordering tax rate, the greater the net smuggling imports will be from the lower-tax neighboring states.
Graphic 3: Unexplained Per-Capita Sales From Naïve Model, 1990-2009
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
Note: Statistical significance of 1 percent, 5 percent and 10 percent are represented by ***, ** and *, respectively.
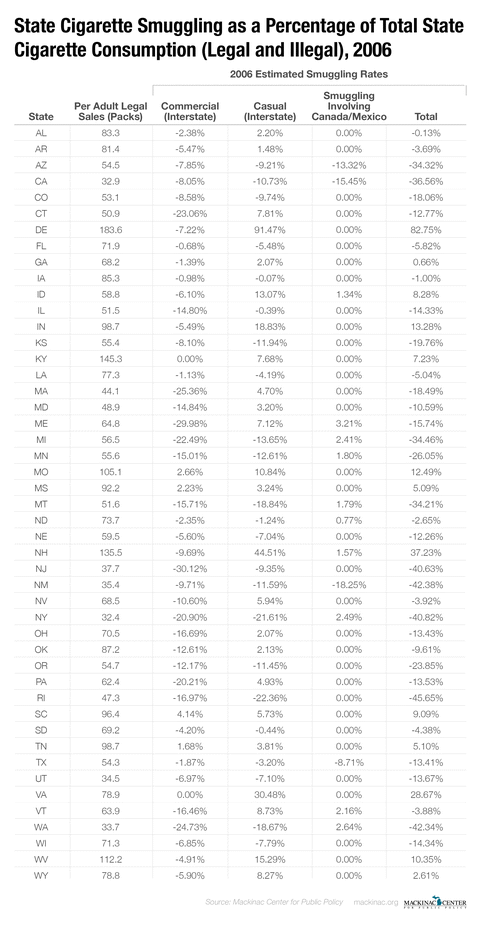
Given the above estimation results, we compute smuggling by type as a percentage of estimated cigarette consumption in the state. Graphic 5 presents our state-level estimates of the percent of estimated cigarette consumption that was smuggled, both by type of smuggling and in total, for 2014, the last year in our dataset. Those states for which the percentage smuggled is negative are net importers of smuggled cigarettes.
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
* Some of the language included in this appendix appears in previously published Mackinac Center reports.
[†]Some evidence suggests a systematic underreporting of cigarette consumption in surveys such as the BRFSS; however, any such bias is likely to impact smoking intensity figures, not smoking prevalence. See Kenneth E Warner, “Possible Increases in the Underreporting of Cigarette Consumption,” Journal of the American Statistical Association 73, no. 362 (1978), https://perma.cc
[††]Admittedly, this figure is not large in economic significance. Nevertheless, the number is statistically significant, and it should be remembered that cross-border casual smuggling is only part of smuggling overall. Commercial smuggling rates respond quickly to cross-border tax differentials, and even with the relatively small percentage impact of tax differentials on casual smuggling, we see that tax changes have a noticeable impact on smuggling, both in total and in each component of smuggling.
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
 Mackinac Center for Public Policy
Mackinac Center for Public Policy
1 James Damask, “Cigarette Smuggling: Financing Terrorism?” (Mackinac Center for Public Policy, July 1, 2002), https://perma.cc
2 “Internet Tobacco Purchases” (Michigan Department of Treasury, Michigan State Police), https://perma.cc
3 “Cigarette Purchases by New York Consumers from Tribal Retailers in New York State (Published in ‘New York Counties Tobacco Trust VI’)” (IHS Global, Inc., Aug. 25, 2016), A-2-13, https://perma4.cc
4 Peter Reuter and Malay Majmundar, eds., “Understanding the U.S. Illicit Tobacco Market: Characteristics, Policy Context, and Lessons from International Experiences” (National Research Council and Institute of Medicine, 2015), Summary-3, https://perma.cc
5 Peter Reuter and Malay Majmundar, eds., “Understanding the U.S. Illicit Tobacco Market: Characteristics, Policy Context, and Lessons from International Experiences” (National Research Council and Institute of Medicine, 2015), 4–20, https://perma.cc
6 Philip DeCicca, Donald Kenkel and Liu Feng, “Reservation Prices: An Economic Analysis of Cigarette Purchases on Indian Reservations,” National Bureau of Economic Research (Dec. 2014), https://perma.cc
7 “Revenue Estimate: Cigarette and Tobacco Products Tax Evasion” (State of California: Board of Equalization, May 2014), https://perma.cc
8 “Study of Wisconsin’s Cigarette Tax Collection System” (Wisconsin Department of Revenue, June 30, 2014), 3, https://perma.cc
9 “Report of Commission on Illegal Tobacco” (Commonwealth of Massachusetts, March 1, 2014), 8–11, https://perma.cc
10 “Cigarette Tax Evasion Estimate - FYI 2013” (Washington State Department of Revenue, March 12, 2014), https://perma.cc
11 “OCSA Contraband Tobacco Ontario Study” (Ontario Convenience Stores Association, Oct. 2014), https://perma.cc
12 “Contraband Tobacco Monitoring Survey Results: Ontario” (National Coalition Against Contraband Tobacco, Sept. 23, 2014), https://perma.cc
13 Brian V Fix et al., “A Novel Approach to Estimating the Prevalence of Untaxed Cigarettes in the USA: Findings from the 2009 and 2010 International Tobacco Control Surveys,” Tobacco Control 23 (Aug. 22, 2013): i61–i66, https://perma.cc
14 Kevin C. Davis et al., “Cigarette Trafficking in Five Northeastern US Cities” (Dec. 11, 2013): 1, https://perma.cc
15 Kevin C. Davis et al., “Cigarette Trafficking in Five Northeastern US Cities” (Dec. 11, 2013): 1–7, https://perma.cc
16 Marin K. Kurti, Klaus von Lampe and Douglas E. Thompkins, “The Illegal Cigarette Market in a Socioeconomically Deprived Inner-City Area: The Case of the South Bronx,” Tobacco Control 22, no. 2 (2013): 1–4, https://perma.cc
17 Edward Olive, deputy sheriff, New York City Department of Finance, email correspondence with Michael LaFaive, director, Morey Fiscal Policy Initiative, Mackinac Center for Public Policy, May 8, 2015.
18 “The State and Local Impact of Tobacco Prices on Smuggling and Black Market Tobacco Sales” (Andrew Chang & Company, Sept. 23, 2013), 26, https://perma.cc
19 “An Examination of Cigarette Sales in New York State by Source: 2011” (John Dunham and Associates, Oct. 10, 2012), https://perma.cc
20 Howard Chernick and David Merriman, “Using Littered Pack Data to Estimate Cigarette Tax Avoidance in New York City,” National Tax Journal 66, no. 2 (June 2013): 8, 11, https://perma.cc
21 Philip DeCicca, Donald S. Kenkel and Feng Liu, “Excise Tax Avoidance: The Case of State Cigarette Taxes,” NBER Working Paper Series (April 2010): Table 2, https://perma.cc
22 Philip DeCicca, Donald S. Kenkel and Feng Liu, “Excise Tax Avoidance: The Case of State Cigarette Taxes,” NBER Working Paper Series (April 2010): 31–32, https://perma.cc
23 David Merriman, “The Micro-Geography of Tax Avoidance: Evidence from Littered Cigarette Packs in Chicago,” American Economic Journal: Economic Policy 2, no. 2 (May 2010): 69–70, https://perma.cc
24 Marsha Blumenthal, “Cigarette Tax Evasion in Minnesota” (Minnesota Department of Revenue, Oct. 18, 2009), 19, https://perma.cc
25 Luk Joossens et al., “How Eliminating the Global Illicit Cigarette Trade Would Increase Tax Revenue and Save Lives” (International Union Against Tuberculosis and Lung Disease, 2009), 12 (Table 4.2), https://perma.cc
26 Michael Lovenheim, “How Far to the Border?: The Extent and Impact of Cross-Border Casual Cigarette Smuggling,” National Tax Journal LXI, no. 1 (March 2008): 7, 10, https://perma.cc
27 Lesley Chiou and Erich Muehlegger, “Crossing the Line: Direct Estimation of Cross-Border Cigarette Sales and the Effect on Tax Revenue,” The B.E. Journal of Economic Analysis & Policy 8, no. 1 (Feb. 2008): 2–3, https://perma.cc
28 Stephen D. Smith and Van Huynh, “Washington State Cigarette Consumption Revisited” (Washington Department of Revenue, Jan. 2007), 25, https://perma.cc
29 Mark Stehr, “Cigarette Tax Avoidance and Evasion,” Journal of Health Economics 24 (2005): 295, https://perma.cc
30 A. Hyland et al., “Higher Cigarette Prices Influence Cigarette Purchase Patterns,” Tobacco Control 14 (2005): 86–92, https://perma.cc
31 Ann Boonn, “Cigarette Tax Increases by State per Year (2000-2017)” (Campaign for Tobacco-Free Kids, Nov. 10, 2016), https://perma.cc
32 Ann Boonn, “Cigarette Tax Increases by State per Year (2000-2017)” (Campaign for Tobacco-Free Kids, Nov. 10, 2016), https://perma.cc
33 “The Tax Burden on Tobacco: Historical Compilation” (Orzechowski and Walker, 2014), 11, https://perma.cc
34 Michael LaFaive, Patrick Fleenor and Todd Nesbit, “Cigarette Taxes and Smuggling: A Statistical Analysis and Historical Review” (Mackinac Center for Public Policy, Dec. 2008), 82–84, https://perma.cc
35 Michael LaFaive, Patrick Fleenor and Todd Nesbit, “Cigarette Taxes and Smuggling: A Statistical Analysis and Historical Review” (Mackinac Center for Public Policy, Dec. 2008), 84, https://perma.cc
36 Kyle Lawson, “Massive Untaxed Cigarette Haul Seized on South Shore, Authorities Say,” State Island Advance (SILive.com, Nov. 23, 2016), https://perma.cc
37 Mark Bowes, “Police: North African Native Used Brandermill Store As Front in $1M Cigarette Smuggling Scheme,” Richmond Times-Dispatch, Oct. 26, 2016, https://perma.cc
38 “NOPD Officers, Deputy Indicted in Cigarette Contraband Trafficking Case,” WDSU, Sept. 29, 2016, https://goo.gl
39 Noah Cohen, “Police Uncover Cigarette Sales Scheme in Newark, Authorities Say,” NJ.com (NJ Advance Media, Sept. 28, 2016), https://perma.cc
40 “Tennessee Lawmaker Convicted of Felony Tax Fraud” (The Associated Press, Aug. 8, 2016), https://perma.cc
41 Frank Green, “Cigarette Trafficking Figure Pleads Guilty,” Richmond-Times Dispatch, June 16, 2016, https://perma.cc
42 Mike Plaisance, “Pedro Perez of Holyoke Pleads Not Guilty to Selling Cigarettes Without Government Excise Stamp to Avoid Taxes,” The Republican, May 12, 2016, https://perma.cc
43 Isabel Vincent and Melissa Klein, “Authorities Break up Chinatown Buses Cigarette-Smuggling Ring,” New York Post, May 8, 2016, https://perma.cc
44 Tom Jensen, “Update: XFINITY Driver Allegedly at ‘Top’ of Tobacco, Drug-Smuggling Ring,” Fox Sports, April 1, 2016, https://perma.cc
45 Robert Pozarycki, “Married Couple under Arrest for Keeping Untaxed Cigarettes in a Flushing Home,” Queens Courier, March 4, 2016, https://perma.cc
46 Robert Patrick, “Feds: Missouri-New York Cigarette Smuggling Ring Dodges $20 Million in Taxes,” St. Louis Post-Dispatch2, March 3, 2016, https://perma.cc
47 “N.C. Man Charged Afer Discovery of 20k Packs of Untaxed Cigarettes” (WBAL TV-11, March 1, 2016), https://perma.cc
48 Allison Bourg, “State Nabs 4 People for Smuggling 72,000 Packs of Contraband Tobacco Products” (WMAR, March 3, 2016), https://perma.cc
49 Michael LaFaive, Patrick Fleenor and Todd Nesbit, “Cigarette Taxes and Smuggling: A Statistical Analysis and Historical Review” (Mackinac Center for Public Policy, Dec. 2008), 71, https://perma.cc
50 Michael LaFaive, Patrick Fleenor and Todd Nesbit, “Cigarette Taxes and Smuggling: A Statistical Analysis and Historical Review” (Mackinac Center for Public Policy, Dec. 2008), 72–84, https://perma.cc
51 R. Morris Coats, "A Note on Estimating Cross-Border Effects of State Cigarette Taxes," National Tax Journal 48, no. 4 (1995).
52 Jerry G. Thursby and Marie C. Thursby, "Interstate Cigarette Bootlegging: Extent, Revenue Losses, and Effects of Federal Intervention," National Tax Journal 53, no. 1 (2000).
53 Jerry G. Thursby and Marie C. Thursby, "Interstate Cigarette Bootlegging: Extent, Revenue Losses, and Effects of Federal Intervention," National Tax Journal 53, no. 1 (2000).